Logarithms
Help Questions
Math › Logarithms
Simplify the expression using logarithmic identities.
The expression cannot be simplified
Explanation
The logarithm of a fraction is equal to the logarithm of the numerator minus the logarithm of the denominator.
If we encounter two logarithms with the same base, we can likely combine them. In this case, we can use the reverse of the above identity.
Simplify the expression using logarithmic identities.
The expression cannot be simplified
Explanation
The logarithm of a fraction is equal to the logarithm of the numerator minus the logarithm of the denominator.
If we encounter two logarithms with the same base, we can likely combine them. In this case, we can use the reverse of the above identity.
Simplify the expression using logarithmic identities.
The expression cannot be simplified
Explanation
The logarithm of a fraction is equal to the logarithm of the numerator minus the logarithm of the denominator.
If we encounter two logarithms with the same base, we can likely combine them. In this case, we can use the reverse of the above identity.
Based on the definition of logarithms, what is 
3
100
10
2
4
Explanation
For any equation 


Based on the definition of logarithms, what is 
3
100
10
2
4
Explanation
For any equation 


Based on the definition of logarithms, what is 
3
100
10
2
4
Explanation
For any equation 


What is the value of 

Explanation



What is the value of 

Explanation



What is the value of 

Explanation



Explanation
Most of us don't know what the exponent would be if 



Fortunately we can use the base change rule:
Plug in our given values.


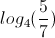












![\sqrt[7]{x}=\sqrt[7]{128}](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1105254/gif.latex)










