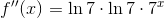Taylor and Maclaurin Series
Help Questions
Math › Taylor and Maclaurin Series
Give the 


Explanation
The 


We can find 
so the 
Give the 
Explanation
The 

The second derivative of 
The coeficient of 
Give the 
Explanation
The 

The second derivative of 
The coeficient of 
Give the 


Explanation
The 


We can find 
so the 
Give the 

Explanation
The 

We can find 
The term we want is therefore
Give the 

Explanation
This can most easily be answered by recalling that the Maclaurin series for 
Multiply by 
The 

Give the 

Explanation
The 

We can find 
The term we want is therefore
Give the 

Explanation
This can most easily be answered by recalling that the Maclaurin series for 
Multiply by 
The 

Give the 

Explanation
The 

We can find 
The coefficient we want is

so the corresponding term is 
Give the 

Explanation
The 

We can find 
The coefficient we want is

so the corresponding term is