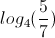Simplifying Logarithms
Help Questions
Math › Simplifying Logarithms
Simplify the expression using logarithmic identities.
The expression cannot be simplified
Explanation
The logarithm of a fraction is equal to the logarithm of the numerator minus the logarithm of the denominator.
If we encounter two logarithms with the same base, we can likely combine them. In this case, we can use the reverse of the above identity.
Which is another way of expressing

Explanation
Use the rule:
therefore
Add the logarithms:
Explanation
When adding logarithms of the same base, all you have to do is multiply the numbers inside the function as shown below:
Simplify the expression using logarithmic identities.
The expression cannot be simplified
Explanation
The logarithm of a fraction is equal to the logarithm of the numerator minus the logarithm of the denominator.
If we encounter two logarithms with the same base, we can likely combine them. In this case, we can use the reverse of the above identity.
Simplify the expression using logarithmic identities.
The expression cannot be simplified
Explanation
The logarithm of a fraction is equal to the logarithm of the numerator minus the logarithm of the denominator.
If we encounter two logarithms with the same base, we can likely combine them. In this case, we can use the reverse of the above identity.
Which is another way of expressing

Explanation
Use the rule:
therefore
Add the logarithms:
Explanation
When adding logarithms of the same base, all you have to do is multiply the numbers inside the function as shown below:
Combine as one log:
Explanation
According to log rules, the coefficients of the logs can be raised as powers for the inner quantity of the log. Rewrite the terms.
Subtract the 
The answer is:
True or false: 

False
True
Explanation
A statement can be proved to not be true in general if one counterexample can be found. One such counterexample assumes that 
becomes
or, equivalently,
The word "log" indicates a common, or base ten, logarithm, as opposed to a natural, or base 

or

This is false, so 

True or false: 

True
False
Explanation
By the Change of Base Property of Logarithms, if 

Substituting 7 for 


The correct choice is "true."