Magnetism and Electromagnetism - MCAT Physical
Card 0 of 91
Which of the following influences the emf produced in a wire loop that is rotating in a magnetic field?
Which of the following influences the emf produced in a wire loop that is rotating in a magnetic field?
Recall that 
, where 
. The shape, material characteristics, and resistance do not appear in this equation. So only the size (area) of the loop influences the emf.
Recall that
Compare your answer with the correct one above
You look at a circular loop of wire such that the plane of the loop is perpendicular to your line of vision. The loop has a constant current that is running through it clockwise. What will happen if a magnetic field were to be activated that is pointing in your direction?
You look at a circular loop of wire such that the plane of the loop is perpendicular to your line of vision. The loop has a constant current that is running through it clockwise. What will happen if a magnetic field were to be activated that is pointing in your direction?
This question works with the concept of induction. Simply put, the current in a wire will adjust such as to oppose a change in magnetic field. The loop originally has a magnetic field pointing away from the observer. Therefore, with the external magnetic field suddenly activated in the opposite direction (towards the observer), the current in the loop will act to counteract this change and increase while remaining clockwise.
This question works with the concept of induction. Simply put, the current in a wire will adjust such as to oppose a change in magnetic field. The loop originally has a magnetic field pointing away from the observer. Therefore, with the external magnetic field suddenly activated in the opposite direction (towards the observer), the current in the loop will act to counteract this change and increase while remaining clockwise.
Compare your answer with the correct one above
Which of the following best describes magnetic field lines?
Which of the following best describes magnetic field lines?
First, magnetic field lines, like electric field lines, can never cross. Also, unlike electric field lines, magnetic field lines are continuous—they do not have starting or ending points. Next, the force experienced by a charge in a magnetic field depends on the charge's velocity direction, not just the magnetic field. So the only remaining choice is that magnetic field lines show both the relative strength and direction of the field.
First, magnetic field lines, like electric field lines, can never cross. Also, unlike electric field lines, magnetic field lines are continuous—they do not have starting or ending points. Next, the force experienced by a charge in a magnetic field depends on the charge's velocity direction, not just the magnetic field. So the only remaining choice is that magnetic field lines show both the relative strength and direction of the field.
Compare your answer with the correct one above
A scientist builds a particle accelerator. Which of the following would not help the scientist increase the speed of a particle in the accelerator?
A scientist builds a particle accelerator. Which of the following would not help the scientist increase the speed of a particle in the accelerator?
A charged particle in a particle accelerator moves in uniform circular motion. The equation for centripetal force caused by uniform circular motion is:
The equation for magnetic force is:
Set the equations equal to each other, and solve for velocity.
The only answer choice that does not correspond to an increase in velocity is increasing the mass of the particles in the accelerator.
A charged particle in a particle accelerator moves in uniform circular motion. The equation for centripetal force caused by uniform circular motion is:
The equation for magnetic force is:
Set the equations equal to each other, and solve for velocity.
The only answer choice that does not correspond to an increase in velocity is increasing the mass of the particles in the accelerator.
Compare your answer with the correct one above
A 
current-carrying wire is placed in a uniform magnetic field oriented perpendicularly to the wire. The length of the wire is 
and the magnitude of the magnetic field is 
. What is the force on the wire?
A
We use the formula for force on a wire in a magnetic field:
Where 
= force, 
= current, 
= length of wire, and 
= magnetic mield
We use the formula for force on a wire in a magnetic field:
Where
Compare your answer with the correct one above
An electron is traveling at constant velocity directed to the the left through a magnetic field directed into the page as shown below.
Which way would the force vector on the electron due to the magnetic field be directed?
An electron is traveling at constant velocity directed to the the left through a magnetic field directed into the page as shown below.
Which way would the force vector on the electron due to the magnetic field be directed?
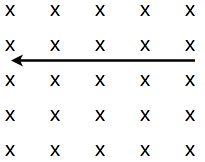
When finding the direction of the force on a POSITIVELY charged particle due to a magnetic field, we can use the right hand rule. Holding your thumb perpendicular to the rest of your fingers (as if motioning to stop), orient your fingers parallel to the lines of the magnetic field, and your thumb with the velocity vector of the charge. For a positive charge, the force would be oriented directly out of the palm; HOWEVER, the charge of an electron is negative and therefore the force will be applied in the opposite direction. This would mean that the force would be coming directly out of the backside of your hand (in this case, towards the top of the page) using the right hand rule.
When finding the direction of the force on a POSITIVELY charged particle due to a magnetic field, we can use the right hand rule. Holding your thumb perpendicular to the rest of your fingers (as if motioning to stop), orient your fingers parallel to the lines of the magnetic field, and your thumb with the velocity vector of the charge. For a positive charge, the force would be oriented directly out of the palm; HOWEVER, the charge of an electron is negative and therefore the force will be applied in the opposite direction. This would mean that the force would be coming directly out of the backside of your hand (in this case, towards the top of the page) using the right hand rule.
Compare your answer with the correct one above
What is the magnitude of force on a 
charge travelling at a constant velocity of 
through a perpendicular 
magnetic field?
What is the magnitude of force on a
The equation for finding the force on a charge in a magnetic field is
F = qvBsinθ
Where q is charge in coulombs, v is the velocity of the charge, and B is the strength of the magnetic field in Teslas. Since the charge is moving perpendicular to the magnetic field, sinθ =1. Therefore we solve for force by plugging in the values and multiplying.
The equation for finding the force on a charge in a magnetic field is
F = qvBsinθ
Where q is charge in coulombs, v is the velocity of the charge, and B is the strength of the magnetic field in Teslas. Since the charge is moving perpendicular to the magnetic field, sinθ =1. Therefore we solve for force by plugging in the values and multiplying.
Compare your answer with the correct one above
A charged particle enters a uniform magnetic field, with velocity v perpendicular to the field, and moves in a circular path of radius R. If the particle's mass were doubled, the radius would become __________.
A charged particle enters a uniform magnetic field, with velocity v perpendicular to the field, and moves in a circular path of radius R. If the particle's mass were doubled, the radius would become __________.
A charged particle's motion in a uniform magnetic field is described by R = mv/qB, so the radius of the particle's path is proportional to its mass. Thus if mass is doubled, radius is also doubled.
A charged particle's motion in a uniform magnetic field is described by R = mv/qB, so the radius of the particle's path is proportional to its mass. Thus if mass is doubled, radius is also doubled.
Compare your answer with the correct one above
In a current-carrying wire, which of the following expressions best relates charge, current, velocity and the length of the wire?
Assume 
is 90o.
In a current-carrying wire, which of the following expressions best relates charge, current, velocity and the length of the wire?
Assume
The force of a charge in a magnetic field is given by the equation 
. q is the charge, v is the velocity, and B is the magnetic field strength.
Additionally, the force on a current-carrying carrying wire in a magnetic field is given by the equation 
. I is the current, L is the length or the wire, and B is the magnetic field strength.
Because we assume the angle to be 90o , we can set the two force equations equal to each other, and derive the equation 
.
By manipulating the variables, we can generate the equation 
. None of the other answer choices can be derived from these equations.
The force of a charge in a magnetic field is given by the equation
Additionally, the force on a current-carrying carrying wire in a magnetic field is given by the equation
Because we assume the angle to be 90o , we can set the two force equations equal to each other, and derive the equation
By manipulating the variables, we can generate the equation
Compare your answer with the correct one above
An electron is moving at a constant velocity due east. It travels from a region of zero magnetic field into a uniform magnetic field of nonzero magnitude and unknown direction. Which of the following could not describe the electron's motion after entering the field?
An electron is moving at a constant velocity due east. It travels from a region of zero magnetic field into a uniform magnetic field of nonzero magnitude and unknown direction. Which of the following could not describe the electron's motion after entering the field?
A magnetic force can accelerate a charged particle by changing the direction of its velocity, but cannot change the magnitude of velocity.
If the magnetic field has any components perpendicular to the particle's initial velocity, the particle will experience a force according to the equation:
This force is generated perpendicular to the particle's path and will cause a change in the direction of the particle's velocity. If the magnetic field is parallel to the initial velocity, the particle will experience no magnetic force, and its path will remain unchanged. It is not possible for the particle to accelerate in the magnetic field without changing direction.
A magnetic force can accelerate a charged particle by changing the direction of its velocity, but cannot change the magnitude of velocity.
If the magnetic field has any components perpendicular to the particle's initial velocity, the particle will experience a force according to the equation:
This force is generated perpendicular to the particle's path and will cause a change in the direction of the particle's velocity. If the magnetic field is parallel to the initial velocity, the particle will experience no magnetic force, and its path will remain unchanged. It is not possible for the particle to accelerate in the magnetic field without changing direction.
Compare your answer with the correct one above
The particle depicted above on the left has a charge of 
and a velocity 
going to the right. What will happen when the particle enters the magnetic field depicted?
The particle depicted above on the left has a charge of
To determine the direction the charge will accelerate, use the right hand rule for magnetic force. To begin, hold out your hand and give a "thumb up," now rotate your wrist 
clockwise so that your thumb is in the direction of the velocity of the charge. Next, extend your index finger so you are pointing into the plane of the page/screen with it, with your palm facing up. Now rotate your wrist so your index finger points in the direction of the magnetic field lines. Now your index finger should be pointing down, with your palm facing the screen/page, and your thumb still pointing to the right. The direction of the magnetic force felt by a positive charge is perpendicularly from your palm outwards, into the plane of the page/screen. Note that if the charge were negative, the direction of the magnetic force felt by the charge would be coming perpendicularly from the top of your hand instead.
To determine the direction the charge will accelerate, use the right hand rule for magnetic force. To begin, hold out your hand and give a "thumb up," now rotate your wrist
Compare your answer with the correct one above
An electron moves at 85km/s to the right along the plane of the page, while a uniform magnetic field points into the page. In what direction does the force act on the moving electron?
An electron moves at 85km/s to the right along the plane of the page, while a uniform magnetic field points into the page. In what direction does the force act on the moving electron?
This question requires knowlegde of the right-hand rule. Point the fingers of your right hand in the direction of the electron's velocity (to the right). Point your thumb in the direction of the magnetic field (into the page). Your palm should be facing in the direction of the force on a positive particle. However, electrons are negative, so this direction must be reversed, meaning that the direction of the force is upward along the plane of the page.
This question requires knowlegde of the right-hand rule. Point the fingers of your right hand in the direction of the electron's velocity (to the right). Point your thumb in the direction of the magnetic field (into the page). Your palm should be facing in the direction of the force on a positive particle. However, electrons are negative, so this direction must be reversed, meaning that the direction of the force is upward along the plane of the page.
Compare your answer with the correct one above
You look at a circular loop of wire such that the plane of the loop is perpendicular to your line of vision. In what direction must a current be going through the loop in order for a magnetic field to be produced in your direction.
You look at a circular loop of wire such that the plane of the loop is perpendicular to your line of vision. In what direction must a current be going through the loop in order for a magnetic field to be produced in your direction.
This is an application of the right hand rule for magnetic fields produced by current carrying loops. To use the right hand rule, put your right thumb in the direction of the current, and the direction of the magnetic field is the same as the way your other four fingers wrap as you close your fist. The answers which include increasing or decreasing of a current hint at the concept of induction and are incorrect.
This is an application of the right hand rule for magnetic fields produced by current carrying loops. To use the right hand rule, put your right thumb in the direction of the current, and the direction of the magnetic field is the same as the way your other four fingers wrap as you close your fist. The answers which include increasing or decreasing of a current hint at the concept of induction and are incorrect.
Compare your answer with the correct one above
Which of the following influences the emf produced in a wire loop that is rotating in a magnetic field?
Which of the following influences the emf produced in a wire loop that is rotating in a magnetic field?
Recall that , where . The shape, material characteristics, and resistance do not appear in this equation. So only the size (area) of the loop influences the emf.
Recall that
Compare your answer with the correct one above
You look at a circular loop of wire such that the plane of the loop is perpendicular to your line of vision. The loop has a constant current that is running through it clockwise. What will happen if a magnetic field were to be activated that is pointing in your direction?
You look at a circular loop of wire such that the plane of the loop is perpendicular to your line of vision. The loop has a constant current that is running through it clockwise. What will happen if a magnetic field were to be activated that is pointing in your direction?
This question works with the concept of induction. Simply put, the current in a wire will adjust such as to oppose a change in magnetic field. The loop originally has a magnetic field pointing away from the observer. Therefore, with the external magnetic field suddenly activated in the opposite direction (towards the observer), the current in the loop will act to counteract this change and increase while remaining clockwise.
This question works with the concept of induction. Simply put, the current in a wire will adjust such as to oppose a change in magnetic field. The loop originally has a magnetic field pointing away from the observer. Therefore, with the external magnetic field suddenly activated in the opposite direction (towards the observer), the current in the loop will act to counteract this change and increase while remaining clockwise.
Compare your answer with the correct one above
Which of the following best describes magnetic field lines?
Which of the following best describes magnetic field lines?
First, magnetic field lines, like electric field lines, can never cross. Also, unlike electric field lines, magnetic field lines are continuous—they do not have starting or ending points. Next, the force experienced by a charge in a magnetic field depends on the charge's velocity direction, not just the magnetic field. So the only remaining choice is that magnetic field lines show both the relative strength and direction of the field.
First, magnetic field lines, like electric field lines, can never cross. Also, unlike electric field lines, magnetic field lines are continuous—they do not have starting or ending points. Next, the force experienced by a charge in a magnetic field depends on the charge's velocity direction, not just the magnetic field. So the only remaining choice is that magnetic field lines show both the relative strength and direction of the field.
Compare your answer with the correct one above
A scientist builds a particle accelerator. Which of the following would not help the scientist increase the speed of a particle in the accelerator?
A scientist builds a particle accelerator. Which of the following would not help the scientist increase the speed of a particle in the accelerator?
A charged particle in a particle accelerator moves in uniform circular motion. The equation for centripetal force caused by uniform circular motion is:
The equation for magnetic force is:
Set the equations equal to each other, and solve for velocity.
The only answer choice that does not correspond to an increase in velocity is increasing the mass of the particles in the accelerator.
A charged particle in a particle accelerator moves in uniform circular motion. The equation for centripetal force caused by uniform circular motion is:
The equation for magnetic force is:
Set the equations equal to each other, and solve for velocity.
The only answer choice that does not correspond to an increase in velocity is increasing the mass of the particles in the accelerator.
Compare your answer with the correct one above
A current-carrying wire is placed in a uniform magnetic field oriented perpendicularly to the wire. The length of the wire is and the magnitude of the magnetic field is . What is the force on the wire?
A
We use the formula for force on a wire in a magnetic field:
Where = force, = current, = length of wire, and = magnetic mield
We use the formula for force on a wire in a magnetic field:
Where
Compare your answer with the correct one above
An electron is traveling at constant velocity directed to the the left through a magnetic field directed into the page as shown below.
Which way would the force vector on the electron due to the magnetic field be directed?
An electron is traveling at constant velocity directed to the the left through a magnetic field directed into the page as shown below.
Which way would the force vector on the electron due to the magnetic field be directed?
When finding the direction of the force on a POSITIVELY charged particle due to a magnetic field, we can use the right hand rule. Holding your thumb perpendicular to the rest of your fingers (as if motioning to stop), orient your fingers parallel to the lines of the magnetic field, and your thumb with the velocity vector of the charge. For a positive charge, the force would be oriented directly out of the palm; HOWEVER, the charge of an electron is negative and therefore the force will be applied in the opposite direction. This would mean that the force would be coming directly out of the backside of your hand (in this case, towards the top of the page) using the right hand rule.
When finding the direction of the force on a POSITIVELY charged particle due to a magnetic field, we can use the right hand rule. Holding your thumb perpendicular to the rest of your fingers (as if motioning to stop), orient your fingers parallel to the lines of the magnetic field, and your thumb with the velocity vector of the charge. For a positive charge, the force would be oriented directly out of the palm; HOWEVER, the charge of an electron is negative and therefore the force will be applied in the opposite direction. This would mean that the force would be coming directly out of the backside of your hand (in this case, towards the top of the page) using the right hand rule.
Compare your answer with the correct one above
What is the magnitude of force on a charge travelling at a constant velocity of through a perpendicular magnetic field?
What is the magnitude of force on a
The equation for finding the force on a charge in a magnetic field is
F = qvBsinθ
Where q is charge in coulombs, v is the velocity of the charge, and B is the strength of the magnetic field in Teslas. Since the charge is moving perpendicular to the magnetic field, sinθ =1. Therefore we solve for force by plugging in the values and multiplying.
The equation for finding the force on a charge in a magnetic field is
F = qvBsinθ
Where q is charge in coulombs, v is the velocity of the charge, and B is the strength of the magnetic field in Teslas. Since the charge is moving perpendicular to the magnetic field, sinθ =1. Therefore we solve for force by plugging in the values and multiplying.
Compare your answer with the correct one above