Electricity and Magnetism - MCAT Physical
Card 0 of 686
Two charges of 
coulombs are a distance 
apart from each other. Which of the following would reduce the force exerted between the charges by a factor of 4?
Two charges of
Given Coulomb's Law electrostatic forces: 
We can see that distance and force are inversly related. Also distance is squared, so if we increase the distance by 2, the force between the two charges will be reduced by a factor of four.
Given Coulomb's Law electrostatic forces:
We can see that distance and force are inversly related. Also distance is squared, so if we increase the distance by 2, the force between the two charges will be reduced by a factor of four.
Compare your answer with the correct one above
How many electrons would it require to generate a 5 N attractive force on a +3 µC charge from 0.1 m away.
How many electrons would it require to generate a 5 N attractive force on a +3 µC charge from 0.1 m away.
To find the answer we must first solve for q, using Coulomb's Law. Then after finding q = 1.85 x 10–6 C, we must divide by 1.6 x 10–19 C to get the amount of electrons required to make such a charge.
To find the answer we must first solve for q, using Coulomb's Law. Then after finding q = 1.85 x 10–6 C, we must divide by 1.6 x 10–19 C to get the amount of electrons required to make such a charge.
Compare your answer with the correct one above
Which of the following influences the emf produced in a wire loop that is rotating in a magnetic field?
Which of the following influences the emf produced in a wire loop that is rotating in a magnetic field?
Recall that 
, where 
. The shape, material characteristics, and resistance do not appear in this equation. So only the size (area) of the loop influences the emf.
Recall that
Compare your answer with the correct one above
You look at a circular loop of wire such that the plane of the loop is perpendicular to your line of vision. The loop has a constant current that is running through it clockwise. What will happen if a magnetic field were to be activated that is pointing in your direction?
You look at a circular loop of wire such that the plane of the loop is perpendicular to your line of vision. The loop has a constant current that is running through it clockwise. What will happen if a magnetic field were to be activated that is pointing in your direction?
This question works with the concept of induction. Simply put, the current in a wire will adjust such as to oppose a change in magnetic field. The loop originally has a magnetic field pointing away from the observer. Therefore, with the external magnetic field suddenly activated in the opposite direction (towards the observer), the current in the loop will act to counteract this change and increase while remaining clockwise.
This question works with the concept of induction. Simply put, the current in a wire will adjust such as to oppose a change in magnetic field. The loop originally has a magnetic field pointing away from the observer. Therefore, with the external magnetic field suddenly activated in the opposite direction (towards the observer), the current in the loop will act to counteract this change and increase while remaining clockwise.
Compare your answer with the correct one above
Which of the following best describes magnetic field lines?
Which of the following best describes magnetic field lines?
First, magnetic field lines, like electric field lines, can never cross. Also, unlike electric field lines, magnetic field lines are continuous—they do not have starting or ending points. Next, the force experienced by a charge in a magnetic field depends on the charge's velocity direction, not just the magnetic field. So the only remaining choice is that magnetic field lines show both the relative strength and direction of the field.
First, magnetic field lines, like electric field lines, can never cross. Also, unlike electric field lines, magnetic field lines are continuous—they do not have starting or ending points. Next, the force experienced by a charge in a magnetic field depends on the charge's velocity direction, not just the magnetic field. So the only remaining choice is that magnetic field lines show both the relative strength and direction of the field.
Compare your answer with the correct one above
A scientist builds a particle accelerator. Which of the following would not help the scientist increase the speed of a particle in the accelerator?
A scientist builds a particle accelerator. Which of the following would not help the scientist increase the speed of a particle in the accelerator?
A charged particle in a particle accelerator moves in uniform circular motion. The equation for centripetal force caused by uniform circular motion is:
The equation for magnetic force is:
Set the equations equal to each other, and solve for velocity.
The only answer choice that does not correspond to an increase in velocity is increasing the mass of the particles in the accelerator.
A charged particle in a particle accelerator moves in uniform circular motion. The equation for centripetal force caused by uniform circular motion is:
The equation for magnetic force is:
Set the equations equal to each other, and solve for velocity.
The only answer choice that does not correspond to an increase in velocity is increasing the mass of the particles in the accelerator.
Compare your answer with the correct one above
A 
current-carrying wire is placed in a uniform magnetic field oriented perpendicularly to the wire. The length of the wire is 
and the magnitude of the magnetic field is 
. What is the force on the wire?
A
We use the formula for force on a wire in a magnetic field:
Where 
= force, 
= current, 
= length of wire, and 
= magnetic mield
We use the formula for force on a wire in a magnetic field:
Where
Compare your answer with the correct one above
An electron is traveling at constant velocity directed to the the left through a magnetic field directed into the page as shown below.
Which way would the force vector on the electron due to the magnetic field be directed?
An electron is traveling at constant velocity directed to the the left through a magnetic field directed into the page as shown below.
Which way would the force vector on the electron due to the magnetic field be directed?
When finding the direction of the force on a POSITIVELY charged particle due to a magnetic field, we can use the right hand rule. Holding your thumb perpendicular to the rest of your fingers (as if motioning to stop), orient your fingers parallel to the lines of the magnetic field, and your thumb with the velocity vector of the charge. For a positive charge, the force would be oriented directly out of the palm; HOWEVER, the charge of an electron is negative and therefore the force will be applied in the opposite direction. This would mean that the force would be coming directly out of the backside of your hand (in this case, towards the top of the page) using the right hand rule.
When finding the direction of the force on a POSITIVELY charged particle due to a magnetic field, we can use the right hand rule. Holding your thumb perpendicular to the rest of your fingers (as if motioning to stop), orient your fingers parallel to the lines of the magnetic field, and your thumb with the velocity vector of the charge. For a positive charge, the force would be oriented directly out of the palm; HOWEVER, the charge of an electron is negative and therefore the force will be applied in the opposite direction. This would mean that the force would be coming directly out of the backside of your hand (in this case, towards the top of the page) using the right hand rule.
Compare your answer with the correct one above
What is the magnitude of force on a 
charge travelling at a constant velocity of 
through a perpendicular 
magnetic field?
What is the magnitude of force on a
The equation for finding the force on a charge in a magnetic field is
F = qvBsinθ
Where q is charge in coulombs, v is the velocity of the charge, and B is the strength of the magnetic field in Teslas. Since the charge is moving perpendicular to the magnetic field, sinθ =1. Therefore we solve for force by plugging in the values and multiplying.
The equation for finding the force on a charge in a magnetic field is
F = qvBsinθ
Where q is charge in coulombs, v is the velocity of the charge, and B is the strength of the magnetic field in Teslas. Since the charge is moving perpendicular to the magnetic field, sinθ =1. Therefore we solve for force by plugging in the values and multiplying.
Compare your answer with the correct one above
A charged particle enters a uniform magnetic field, with velocity v perpendicular to the field, and moves in a circular path of radius R. If the particle's mass were doubled, the radius would become __________.
A charged particle enters a uniform magnetic field, with velocity v perpendicular to the field, and moves in a circular path of radius R. If the particle's mass were doubled, the radius would become __________.
A charged particle's motion in a uniform magnetic field is described by R = mv/qB, so the radius of the particle's path is proportional to its mass. Thus if mass is doubled, radius is also doubled.
A charged particle's motion in a uniform magnetic field is described by R = mv/qB, so the radius of the particle's path is proportional to its mass. Thus if mass is doubled, radius is also doubled.
Compare your answer with the correct one above
In a current-carrying wire, which of the following expressions best relates charge, current, velocity and the length of the wire?
Assume 
is 90o.
In a current-carrying wire, which of the following expressions best relates charge, current, velocity and the length of the wire?
Assume
The force of a charge in a magnetic field is given by the equation 
. q is the charge, v is the velocity, and B is the magnetic field strength.
Additionally, the force on a current-carrying carrying wire in a magnetic field is given by the equation 
. I is the current, L is the length or the wire, and B is the magnetic field strength.
Because we assume the angle to be 90o , we can set the two force equations equal to each other, and derive the equation 
.
By manipulating the variables, we can generate the equation 
. None of the other answer choices can be derived from these equations.
The force of a charge in a magnetic field is given by the equation
Additionally, the force on a current-carrying carrying wire in a magnetic field is given by the equation
Because we assume the angle to be 90o , we can set the two force equations equal to each other, and derive the equation
By manipulating the variables, we can generate the equation
Compare your answer with the correct one above
An electron is moving at a constant velocity due east. It travels from a region of zero magnetic field into a uniform magnetic field of nonzero magnitude and unknown direction. Which of the following could not describe the electron's motion after entering the field?
An electron is moving at a constant velocity due east. It travels from a region of zero magnetic field into a uniform magnetic field of nonzero magnitude and unknown direction. Which of the following could not describe the electron's motion after entering the field?
A magnetic force can accelerate a charged particle by changing the direction of its velocity, but cannot change the magnitude of velocity.
If the magnetic field has any components perpendicular to the particle's initial velocity, the particle will experience a force according to the equation:
This force is generated perpendicular to the particle's path and will cause a change in the direction of the particle's velocity. If the magnetic field is parallel to the initial velocity, the particle will experience no magnetic force, and its path will remain unchanged. It is not possible for the particle to accelerate in the magnetic field without changing direction.
A magnetic force can accelerate a charged particle by changing the direction of its velocity, but cannot change the magnitude of velocity.
If the magnetic field has any components perpendicular to the particle's initial velocity, the particle will experience a force according to the equation:
This force is generated perpendicular to the particle's path and will cause a change in the direction of the particle's velocity. If the magnetic field is parallel to the initial velocity, the particle will experience no magnetic force, and its path will remain unchanged. It is not possible for the particle to accelerate in the magnetic field without changing direction.
Compare your answer with the correct one above
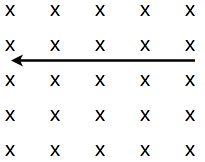
The particle depicted above on the left has a charge of 
and a velocity 
going to the right. What will happen when the particle enters the magnetic field depicted?
The particle depicted above on the left has a charge of
To determine the direction the charge will accelerate, use the right hand rule for magnetic force. To begin, hold out your hand and give a "thumb up," now rotate your wrist 
clockwise so that your thumb is in the direction of the velocity of the charge. Next, extend your index finger so you are pointing into the plane of the page/screen with it, with your palm facing up. Now rotate your wrist so your index finger points in the direction of the magnetic field lines. Now your index finger should be pointing down, with your palm facing the screen/page, and your thumb still pointing to the right. The direction of the magnetic force felt by a positive charge is perpendicularly from your palm outwards, into the plane of the page/screen. Note that if the charge were negative, the direction of the magnetic force felt by the charge would be coming perpendicularly from the top of your hand instead.
To determine the direction the charge will accelerate, use the right hand rule for magnetic force. To begin, hold out your hand and give a "thumb up," now rotate your wrist
Compare your answer with the correct one above
An electron moves at 85km/s to the right along the plane of the page, while a uniform magnetic field points into the page. In what direction does the force act on the moving electron?
An electron moves at 85km/s to the right along the plane of the page, while a uniform magnetic field points into the page. In what direction does the force act on the moving electron?
This question requires knowlegde of the right-hand rule. Point the fingers of your right hand in the direction of the electron's velocity (to the right). Point your thumb in the direction of the magnetic field (into the page). Your palm should be facing in the direction of the force on a positive particle. However, electrons are negative, so this direction must be reversed, meaning that the direction of the force is upward along the plane of the page.
This question requires knowlegde of the right-hand rule. Point the fingers of your right hand in the direction of the electron's velocity (to the right). Point your thumb in the direction of the magnetic field (into the page). Your palm should be facing in the direction of the force on a positive particle. However, electrons are negative, so this direction must be reversed, meaning that the direction of the force is upward along the plane of the page.
Compare your answer with the correct one above
You look at a circular loop of wire such that the plane of the loop is perpendicular to your line of vision. In what direction must a current be going through the loop in order for a magnetic field to be produced in your direction.
You look at a circular loop of wire such that the plane of the loop is perpendicular to your line of vision. In what direction must a current be going through the loop in order for a magnetic field to be produced in your direction.
This is an application of the right hand rule for magnetic fields produced by current carrying loops. To use the right hand rule, put your right thumb in the direction of the current, and the direction of the magnetic field is the same as the way your other four fingers wrap as you close your fist. The answers which include increasing or decreasing of a current hint at the concept of induction and are incorrect.
This is an application of the right hand rule for magnetic fields produced by current carrying loops. To use the right hand rule, put your right thumb in the direction of the current, and the direction of the magnetic field is the same as the way your other four fingers wrap as you close your fist. The answers which include increasing or decreasing of a current hint at the concept of induction and are incorrect.
Compare your answer with the correct one above
Two charges Q1 and Q2 are held stationary 1 m away from each other. The magnitude of charge of Q2 is twice that of Q1. A positive point charge A is placed directly in the middle of the two charges (Q1 and Q2). What is the ratio of the net force on charge A when Q1 and Q2 are both negative over the net force on charge A when Q1 is negative and Q2 is positive?
Two charges Q1 and Q2 are held stationary 1 m away from each other. The magnitude of charge of Q2 is twice that of Q1. A positive point charge A is placed directly in the middle of the two charges (Q1 and Q2). What is the ratio of the net force on charge A when Q1 and Q2 are both negative over the net force on charge A when Q1 is negative and Q2 is positive?
For this problem we must understand Coulomb's Law. The force on charge A will be dircetly affected by the charge of Q1 and Q2. Q1 and Q2 are both negative, they will both attract charge A, and the net force will be reduced as they pull in opposite directions. Switching Q2 to a positive charge will result in a repulsive force on charge A which will be in the same direction as the attractive force between Q1 and A.
For this problem we must understand Coulomb's Law. The force on charge A will be dircetly affected by the charge of Q1 and Q2. Q1 and Q2 are both negative, they will both attract charge A, and the net force will be reduced as they pull in opposite directions. Switching Q2 to a positive charge will result in a repulsive force on charge A which will be in the same direction as the attractive force between Q1 and A.
Compare your answer with the correct one above
Two point charges, Q1 and Q2, are placed on the x-axis. Q1 is placed at x = 0m and Q2 at x = 1m. If a positive charge, Q3, is placed on the x-axis at x = 0.25m, it experiences a net electric force of 0. Which of the following could be determined based on this observation?
Two point charges, Q1 and Q2, are placed on the x-axis. Q1 is placed at x = 0m and Q2 at x = 1m. If a positive charge, Q3, is placed on the x-axis at x = 0.25m, it experiences a net electric force of 0. Which of the following could be determined based on this observation?
In order for there to be 0 net force on Q3, the forces from Q1 and Q2 must be in opposite directions. So Q1 and Q2 must either be both attracting Q3 or both repelling Q3 (that is, Q1 and Q2 are either both negative or both positive).
Also, since these forces must have equal magnitude in order to cancel, such that 
, where 
is the magnitude of force between Q1 and Q3, and similarly for 
. Recalling Coulomb’s law for electric force, 
and 
(where Q1, Q2, and Q3 are the magnitudes of the respective charges). Since 
, it must also be true that 
for the two fractions to have the same value. So, Q2 must have a greater magnitude than Q1.
In order for there to be 0 net force on Q3, the forces from Q1 and Q2 must be in opposite directions. So Q1 and Q2 must either be both attracting Q3 or both repelling Q3 (that is, Q1 and Q2 are either both negative or both positive).
Also, since these forces must have equal magnitude in order to cancel, such that
Compare your answer with the correct one above
Electronegativity is an important concept in physical chemistry, and often used to help quantify the dipole moment of polar compounds. Polar compounds are different from those compounds that are purely nonpolar or purely ionic. An example can be seen by contrasting sodium chloride, NaCl, with an organic molecule, R-C-OH. The former is purely ionic, and the latter is polar covalent.
When comparing more than one polar covalent molecule, we use the dipole moment value to help us determine relative strength of polarity. Dipole moment, however, is dependent on the electronegativity of the atoms making up the bond. Electronegativity is a property inherent to the atom in question, whereas dipole moment is a property of the bond between them.
For example, oxygen has an electronegativity of 3.44, and hydrogen of 2.20. In other words, oxygen more strongly attracts electrons when in a bond with hydrogen. This leads to the O-H bond having a dipole moment.
When all the dipole moments of polar bonds in a molecule are summed, the molecular dipole moment results, as per the following equation.
Dipole moment = charge * separation distance
Electronegativity is based on the principle that the closer an electron is to the atomic nucleus, where postive charge is concentrated, the more attractive force the positive charge can exert on the electron.
As a result, as atomic radius decreases by one half, what happens to the force pulling the electron toward that atom?
Electronegativity is an important concept in physical chemistry, and often used to help quantify the dipole moment of polar compounds. Polar compounds are different from those compounds that are purely nonpolar or purely ionic. An example can be seen by contrasting sodium chloride, NaCl, with an organic molecule, R-C-OH. The former is purely ionic, and the latter is polar covalent.
When comparing more than one polar covalent molecule, we use the dipole moment value to help us determine relative strength of polarity. Dipole moment, however, is dependent on the electronegativity of the atoms making up the bond. Electronegativity is a property inherent to the atom in question, whereas dipole moment is a property of the bond between them.
For example, oxygen has an electronegativity of 3.44, and hydrogen of 2.20. In other words, oxygen more strongly attracts electrons when in a bond with hydrogen. This leads to the O-H bond having a dipole moment.
When all the dipole moments of polar bonds in a molecule are summed, the molecular dipole moment results, as per the following equation.
Dipole moment = charge * separation distance
Electronegativity is based on the principle that the closer an electron is to the atomic nucleus, where postive charge is concentrated, the more attractive force the positive charge can exert on the electron.
As a result, as atomic radius decreases by one half, what happens to the force pulling the electron toward that atom?
This is a function of the equation 
.
In other words, as the distance between two charges doubles, the force between them goes increases, as the denominator decreases from 
to 
.
Here, we are decreasing the distance by 1/2, decreasing the denominator by 1/4, so our force goes up by 4 times.
This is a function of the equation
In other words, as the distance between two charges doubles, the force between them goes increases, as the denominator decreases from
Here, we are decreasing the distance by 1/2, decreasing the denominator by 1/4, so our force goes up by 4 times.
Compare your answer with the correct one above
Batteries and AC current are often used to charge a capacitor. A common example of capacitor use is in computer hard drives, where capacitors are charged in a specific pattern to code information. A simplified circuit with capacitors can be seen below. The capacitance of C1 is 0.5 μF and the capacitances of C2 and C3 are 1 μF each. A 10 V battery with an internal resistance of 1 Ω supplies the circuit.
Using the plate diagram above, what direction do the electric field lines point?
Batteries and AC current are often used to charge a capacitor. A common example of capacitor use is in computer hard drives, where capacitors are charged in a specific pattern to code information. A simplified circuit with capacitors can be seen below. The capacitance of C1 is 0.5 μF and the capacitances of C2 and C3 are 1 μF each. A 10 V battery with an internal resistance of 1 Ω supplies the circuit.
Using the plate diagram above, what direction do the electric field lines point?
As with a point charge, remember that electric field lines point from areas of high potential to areas of low potential. Areas of high potential have positive (+) charge and areas of low potential have negative (-) charge, thus the electric field lines point to the right.
As with a point charge, remember that electric field lines point from areas of high potential to areas of low potential. Areas of high potential have positive (+) charge and areas of low potential have negative (-) charge, thus the electric field lines point to the right.
Compare your answer with the correct one above
Batteries and AC current are often used to charge a capacitor. A common example of capacitor use is in computer hard drives, where capacitors are charged in a specific pattern to code information. A simplified circuit with capacitors can be seen below. The capacitance of C1 is 0.5 μF and the capacitances of C2 and C3 are 1 μF each. A 10 V battery with an internal resistance of 1 Ω supplies the circuit.
Using the plate diagram above, in what direction do the electric force lines point?
Batteries and AC current are often used to charge a capacitor. A common example of capacitor use is in computer hard drives, where capacitors are charged in a specific pattern to code information. A simplified circuit with capacitors can be seen below. The capacitance of C1 is 0.5 μF and the capacitances of C2 and C3 are 1 μF each. A 10 V battery with an internal resistance of 1 Ω supplies the circuit.
Using the plate diagram above, in what direction do the electric force lines point?
As with a point charge, remember that electric force lines point away from positive charge and towards negative charge. As can be seen in the image, electric force lines point to the right. As an aside, electric field lines point in the same direction as electric force lines, so if you know the direction of one, you also know the direction of the other.
As with a point charge, remember that electric force lines point away from positive charge and towards negative charge. As can be seen in the image, electric force lines point to the right. As an aside, electric field lines point in the same direction as electric force lines, so if you know the direction of one, you also know the direction of the other.
Compare your answer with the correct one above