Energy - Physics
Card 0 of 268
Laurence throws a 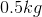 rock off the edge of a
rock off the edge of a  tall building at an angle of
tall building at an angle of  from the horizontal with an initial speed of
from the horizontal with an initial speed of  .
.
 .
.
What is the vertical kinetic energy right before the rock hits the ground?
Laurence throws a 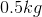




What is the vertical kinetic energy right before the rock hits the ground?
The formula for kinetic energy is:

Since the velocity we're working with is going to be in the vertical direction, we need to find the final  . The best place to start is by finding the initial vertical velocity. To do that, we need to break the given velocity into its vertical component by using the sine function and the angle.
. The best place to start is by finding the initial vertical velocity. To do that, we need to break the given velocity into its vertical component by using the sine function and the angle.
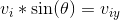



We know that the rock is going to travel a net of  , as that's the displacement between the rock's initial position (on the building) and the ground. Using the appropriate motion equation, we can find the final velocity using the initial velocity, displacement, and acceleration.
, as that's the displacement between the rock's initial position (on the building) and the ground. Using the appropriate motion equation, we can find the final velocity using the initial velocity, displacement, and acceleration.

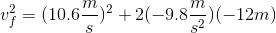




Use this final vertical velocity and the mass of the rock to calculate the final kinetic energy in the vertical direction.



The formula for kinetic energy is:
Since the velocity we're working with is going to be in the vertical direction, we need to find the final 
We know that the rock is going to travel a net of 
Use this final vertical velocity and the mass of the rock to calculate the final kinetic energy in the vertical direction.
Compare your answer with the correct one above
Sam throws a  rock off the edge of a
rock off the edge of a  tall building at an angle of
tall building at an angle of  from the horizontal. The rock has an initial speed of
from the horizontal. The rock has an initial speed of  .
.

What is the total vertical mechanical energy as the rock leaves Sam's hand?
Sam throws a 



What is the total vertical mechanical energy as the rock leaves Sam's hand?
Total mechanical energy is the sum of potential energy and mechanical energy.

We can expand this equation to include the formulas for kinetic and potential energy.

Since we are only looking at vertical energies, we need to find the initial vertical velocity to apply toward the kinetic energy.
To find the vertical velocity we use the equation  .
.
We can plug in the given values for the angle and initial velocity to solve.



Now we have all the terms necessary to solve for the total energy. Keep in mind that the change in height is going to be negative, since the rock is traveling downward.



Total mechanical energy is the sum of potential energy and mechanical energy.
We can expand this equation to include the formulas for kinetic and potential energy.
Since we are only looking at vertical energies, we need to find the initial vertical velocity to apply toward the kinetic energy.
To find the vertical velocity we use the equation 
We can plug in the given values for the angle and initial velocity to solve.
Now we have all the terms necessary to solve for the total energy. Keep in mind that the change in height is going to be negative, since the rock is traveling downward.
Compare your answer with the correct one above
A  book falls off the top of a
book falls off the top of a  bookshelf. What is its kinetic energy right before it hits the ground?
bookshelf. What is its kinetic energy right before it hits the ground?

A 

Remember the law of conservation of energy: the total energy at the beginning equals the total energy at the end. In this case, we have only potential energy at the beginning and only kinetic energy at the end. (The initial velocity is zero, and the final height is zero).

If we can find the potential energy, we can find the kinetic energy. The formula for potential energy is  .
.
Using our given values for the mass, height, and gravity, we can solve using multiplication. Note that the height becomes negative because the book is traveling in the downward direction.


The kinetic energy will also equal  , due to conservation of energy.
, due to conservation of energy.
Remember the law of conservation of energy: the total energy at the beginning equals the total energy at the end. In this case, we have only potential energy at the beginning and only kinetic energy at the end. (The initial velocity is zero, and the final height is zero).
If we can find the potential energy, we can find the kinetic energy. The formula for potential energy is 
Using our given values for the mass, height, and gravity, we can solve using multiplication. Note that the height becomes negative because the book is traveling in the downward direction.
The kinetic energy will also equal 
Compare your answer with the correct one above
A  book falls off the top of a
book falls off the top of a  bookshelf. What is its kinetic energy right before it hits the ground?
bookshelf. What is its kinetic energy right before it hits the ground?

A 

Remember the law of conservation of energy: the total energy at the beginning equals the total energy at the end. In this case, we have only potential energy at the beginning and only kinetic energy at the end. (The initial velocity is zero, and the final height is zero).

If we can find the potential energy, we can find the kinetic energy. The formula for potential energy is  .
.
Using our given values for the mass, height, and gravity, we can solve using multiplication. Note that the height becomes negative because the book is traveling in the downward direction.


The kinetic energy will also equal  , due to conservation of energy.
, due to conservation of energy.
Remember the law of conservation of energy: the total energy at the beginning equals the total energy at the end. In this case, we have only potential energy at the beginning and only kinetic energy at the end. (The initial velocity is zero, and the final height is zero).
If we can find the potential energy, we can find the kinetic energy. The formula for potential energy is 
Using our given values for the mass, height, and gravity, we can solve using multiplication. Note that the height becomes negative because the book is traveling in the downward direction.
The kinetic energy will also equal 
Compare your answer with the correct one above
A man stands on a tall ladder of height  . He leans over a little too far and falls off the ladder. If his mass is
. He leans over a little too far and falls off the ladder. If his mass is  , what is his potential energy right before he falls?
, what is his potential energy right before he falls?
A man stands on a tall ladder of height 

The potential energy at a given height it the product of the height, the mass of the object, and the acceleration of gravity.
Potential gravitational energy is given from the equation:

The potential energy at a given height it the product of the height, the mass of the object, and the acceleration of gravity.
Potential gravitational energy is given from the equation:
Compare your answer with the correct one above
A man stands on a tall ladder of height  . He leans over a little too far and falls off the ladder. If his mass is
. He leans over a little too far and falls off the ladder. If his mass is  , what is his velocity right before he hits the ground?
, what is his velocity right before he hits the ground?
A man stands on a tall ladder of height 

For this problem, use the law of conservation of energy. This states that the total energy before the fall will equal the total energy after the fall. The initial kinetic energy will be zero, and the final potential energy will be zero; thus, the initial non-zero potential energy will be equal to the final non-zero kinetic energy.


From there, expand the equation to include the individual formulas for potential and kinetic energy calculation.

Notice that the mass will cancel out from both sides.

Now we can solve for the final velocity in terms of the initial height.



For this problem, use the law of conservation of energy. This states that the total energy before the fall will equal the total energy after the fall. The initial kinetic energy will be zero, and the final potential energy will be zero; thus, the initial non-zero potential energy will be equal to the final non-zero kinetic energy.
From there, expand the equation to include the individual formulas for potential and kinetic energy calculation.
Notice that the mass will cancel out from both sides.
Now we can solve for the final velocity in terms of the initial height.
Compare your answer with the correct one above
A ball drops from a height  . What more do we need to calculate initial potential energy?
. What more do we need to calculate initial potential energy?
A ball drops from a height 
The formula for potential energy is:

Since  is a constant, the acceleration due to gravity on Earth, we only need the mass and the height. The problem gives a height, so we only need mass.
is a constant, the acceleration due to gravity on Earth, we only need the mass and the height. The problem gives a height, so we only need mass.
Given the mass and the height, we would be able to calculate the initial potential energy.
The formula for potential energy is:
Since 
Given the mass and the height, we would be able to calculate the initial potential energy.
Compare your answer with the correct one above
A runner arrives at the bottom of a hill. He runs up the hill with a constant acceleration until he reaches the top, then runs at a steady pace along the top of the hill. When are the kinetic and potential energies of this man at their greatest?
A runner arrives at the bottom of a hill. He runs up the hill with a constant acceleration until he reaches the top, then runs at a steady pace along the top of the hill. When are the kinetic and potential energies of this man at their greatest?
To answer this question, we can address each type of energy separately. There is no conservation of energy in this problem; kinetic energy is not converted to potential energy as the man runs up the hill. Instead, he is accelerating, indicating an outside force that disallows conservation of energy.
First, we will find the maximum potential energy using the equation:

The man's mass and the acceleration of gravity will remain constant. The only changing variable is height. When the height is greatest, the potential energy will be the greatest. We can conclude that the potential energy will thus be greatest at the top of the hill.
Now we will look at the equation for kinetic energy:

The man's mass will remain constant, and the only changing variable will be the velocity. We are told that the man accelerates as he runs up the hill, indicating that his velocity is increasing. This tells us that he will reach a maximum velocity when he reaches the top of the hill, at which point he maintains a steady velocity along the top of the hill. Since kinetic energy is at a maximum when velocity is at a maximum, we can conclude that kinetic energy is greatest at the top of the hill.
To answer this question, we can address each type of energy separately. There is no conservation of energy in this problem; kinetic energy is not converted to potential energy as the man runs up the hill. Instead, he is accelerating, indicating an outside force that disallows conservation of energy.
First, we will find the maximum potential energy using the equation:
The man's mass and the acceleration of gravity will remain constant. The only changing variable is height. When the height is greatest, the potential energy will be the greatest. We can conclude that the potential energy will thus be greatest at the top of the hill.
Now we will look at the equation for kinetic energy:
The man's mass will remain constant, and the only changing variable will be the velocity. We are told that the man accelerates as he runs up the hill, indicating that his velocity is increasing. This tells us that he will reach a maximum velocity when he reaches the top of the hill, at which point he maintains a steady velocity along the top of the hill. Since kinetic energy is at a maximum when velocity is at a maximum, we can conclude that kinetic energy is greatest at the top of the hill.
Compare your answer with the correct one above
A ball is dropped from  above the ground. Assuming gravity is
above the ground. Assuming gravity is  , what is its final velocity?
, what is its final velocity?
A ball is dropped from 

We can use potential energy to solve. Remember, your height and your gravity need to have the same sign, as they are moving in the same direction (downward). Either make them both negative, or use an absolute value.
Using conservation of energy, we know that  . This tells us that the potential energy at the top of the hill is all converted to kinetic energy at the bottom of the hill. We can substitute the equations for potential energy and kinetic energy.
. This tells us that the potential energy at the top of the hill is all converted to kinetic energy at the bottom of the hill. We can substitute the equations for potential energy and kinetic energy.

The masses cancel out.

Plug in the values, and solve for the velocity.





We can use potential energy to solve. Remember, your height and your gravity need to have the same sign, as they are moving in the same direction (downward). Either make them both negative, or use an absolute value.
Using conservation of energy, we know that 
The masses cancel out.
Plug in the values, and solve for the velocity.
Compare your answer with the correct one above
A pendulum with string length  is dropped from rest. If the mass at the end of the pendulum is
is dropped from rest. If the mass at the end of the pendulum is  , what is its maximum velocity?
, what is its maximum velocity?

A pendulum with string length 

The maximum velocity of the pendulum will be when the object has only kinetic energy. Using conservation of energy, we can set our initial potential energy to equal our "final" kinetic energy.


Plug in the given values and solve for the velocity.





The maximum velocity of the pendulum will be when the object has only kinetic energy. Using conservation of energy, we can set our initial potential energy to equal our "final" kinetic energy.
Plug in the given values and solve for the velocity.
Compare your answer with the correct one above
A  ball rolls down a
ball rolls down a  hill with an initial velocity of
hill with an initial velocity of  . What is its maximum velocity?
. What is its maximum velocity?

A 


For this problem, the ball starts with both potential and kinetic energy. The point of maximum velocity will have no potential energy. We can solve setting the initial energy and final energy equal, due to conservation of energy.


The masses will cancel out from all of the terms.

Plug in the given values and solve for the final velocity. Remember, when the ball is on the ground it has a height of zero.






For this problem, the ball starts with both potential and kinetic energy. The point of maximum velocity will have no potential energy. We can solve setting the initial energy and final energy equal, due to conservation of energy.
The masses will cancel out from all of the terms.
Plug in the given values and solve for the final velocity. Remember, when the ball is on the ground it has a height of zero.
Compare your answer with the correct one above
A rock is dropped from a helicopter hovering at  above the ground. If the rock weighs
above the ground. If the rock weighs  , what is its kinetic energy right before it hits the ground?
, what is its kinetic energy right before it hits the ground?
A rock is dropped from a helicopter hovering at 

Right before it hits the ground, the initial potential energy and the final kinetic energy will equal each other due to conservation of energy.

If we solve for initial potential, we can find final kinetic energy.

Plug in the values given. Remember that height is the change in height. Since the rock is headed downward, the height will be negative.

Multiply and solve.

Right before it hits the ground, the initial potential energy and the final kinetic energy will equal each other due to conservation of energy.
If we solve for initial potential, we can find final kinetic energy.
Plug in the values given. Remember that height is the change in height. Since the rock is headed downward, the height will be negative.
Multiply and solve.
Compare your answer with the correct one above
A book falls off of a  high table. If the book weighs
high table. If the book weighs  , what will its kinetic energy be right before it hits the ground?
, what will its kinetic energy be right before it hits the ground?

A book falls off of a 

Initially, the book has only potential energy. Right before it hits the ground, all the potential energy will have converted to kinetic energy. The two values will be equal based on the conservation of energy.

If we solve for potential, we can find kinetic energy.



Initially, the book has only potential energy. Right before it hits the ground, all the potential energy will have converted to kinetic energy. The two values will be equal based on the conservation of energy.
If we solve for potential, we can find kinetic energy.
Compare your answer with the correct one above
A book falls off of a  high table. If the book weighs
high table. If the book weighs  , what will its final velocity be right before it hits the ground?
, what will its final velocity be right before it hits the ground?

A book falls off of a 

The book initially has only potential energy. Right before it hits the ground, all the potential energy will be converted to kinetic energy. We can use the law of conservation of energy to set the initial and final energies equal.

Use the equations for potential energy and kinetic energy.

Now, plug in the values given to you in the problem and solve for the velocity.






The book initially has only potential energy. Right before it hits the ground, all the potential energy will be converted to kinetic energy. We can use the law of conservation of energy to set the initial and final energies equal.
Use the equations for potential energy and kinetic energy.
Now, plug in the values given to you in the problem and solve for the velocity.
Compare your answer with the correct one above
Sam throws a  rock off the edge of a
rock off the edge of a  tall building at an angle of
tall building at an angle of  from the horizontal. The rock has an initial speed of
from the horizontal. The rock has an initial speed of  .
.

What is the final vertical kinetic energy right before the rock hits the ground?
Sam throws a 



What is the final vertical kinetic energy right before the rock hits the ground?
The formula for kinetic energy is  .
.
We first need to find the initial velocity in the vertical direction. To find the vertical velocity we use the equation  .
.
We can plug in the given values for the angle and initial velocity to solve.



We know that the rock is going to travel a net distance of  , as that is the distance between where the rock's initial and final positions. We now know the displacement, initial velocity, and acceleration, which will allow us to solve for the final velocity.
, as that is the distance between where the rock's initial and final positions. We now know the displacement, initial velocity, and acceleration, which will allow us to solve for the final velocity.






Now we have the mass and final velocity, allowing us to solve for the final kinetic energy.



The formula for kinetic energy is 
We first need to find the initial velocity in the vertical direction. To find the vertical velocity we use the equation 
We can plug in the given values for the angle and initial velocity to solve.
We know that the rock is going to travel a net distance of 
Now we have the mass and final velocity, allowing us to solve for the final kinetic energy.
Compare your answer with the correct one above
A  book falls off the top of a
book falls off the top of a  bookshelf. What is its velocity right before it hits the ground?
bookshelf. What is its velocity right before it hits the ground?

A 

The relationship between velocity and energy is:

We know the mass, but we need to find the total kinetic energy.
Remember the law of conservation of energy: the total energy at the beginning equals the total energy at the end. In this case, we have only potential energy at the beginning and only kinetic energy at the end. (The initial velocity is zero, and the final height is zero).

If we can find the potential energy, we can find the kinetic energy. The formula for potential energy is 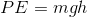 .
.
Using our given values for the mass, height, and gravity, we can solve using multiplication. Note that the height becomes negative because the book is traveling in the downward direction.


The kinetic energy will also equal  , due to conservation of energy.
, due to conservation of energy.
Using this value and our given mass, we can calculate the velocity from our original kinetic energy equation.

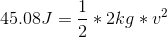



Since we are taking the square root, our answer can be either negative or positive. The final velocity of the book will be in the downward direction; thus, our final velocity should be negative.

The relationship between velocity and energy is:
We know the mass, but we need to find the total kinetic energy.
Remember the law of conservation of energy: the total energy at the beginning equals the total energy at the end. In this case, we have only potential energy at the beginning and only kinetic energy at the end. (The initial velocity is zero, and the final height is zero).
If we can find the potential energy, we can find the kinetic energy. The formula for potential energy is 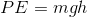
Using our given values for the mass, height, and gravity, we can solve using multiplication. Note that the height becomes negative because the book is traveling in the downward direction.
The kinetic energy will also equal 
Using this value and our given mass, we can calculate the velocity from our original kinetic energy equation.
Since we are taking the square root, our answer can be either negative or positive. The final velocity of the book will be in the downward direction; thus, our final velocity should be negative.
Compare your answer with the correct one above
A  book falls off the top of a
book falls off the top of a  bookshelf. What is its velocity right before it hits the ground?
bookshelf. What is its velocity right before it hits the ground?

A 

The relationship between velocity and energy is:

We know the mass, but we need to find the total kinetic energy.
Remember the law of conservation of energy: the total energy at the beginning equals the total energy at the end. In this case, we have only potential energy at the beginning and only kinetic energy at the end. (The initial velocity is zero, and the final height is zero).

If we can find the potential energy, we can find the kinetic energy. The formula for potential energy is  .
.
Using our given values for the mass, height, and gravity, we can solve using multiplication. Note that the height becomes negative because the book is traveling in the downward direction.


The kinetic energy will also equal  , due to conservation of energy.
, due to conservation of energy.
Using this value and our given mass, we can calculate the velocity from our original kinetic energy equation.






Since we are taking the square root, our answer can be either negative or positive. The final velocity of the book will be in the downward direction; thus, our final velocity should be negative.

The relationship between velocity and energy is:
We know the mass, but we need to find the total kinetic energy.
Remember the law of conservation of energy: the total energy at the beginning equals the total energy at the end. In this case, we have only potential energy at the beginning and only kinetic energy at the end. (The initial velocity is zero, and the final height is zero).
If we can find the potential energy, we can find the kinetic energy. The formula for potential energy is 
Using our given values for the mass, height, and gravity, we can solve using multiplication. Note that the height becomes negative because the book is traveling in the downward direction.
The kinetic energy will also equal 
Using this value and our given mass, we can calculate the velocity from our original kinetic energy equation.
Since we are taking the square root, our answer can be either negative or positive. The final velocity of the book will be in the downward direction; thus, our final velocity should be negative.
Compare your answer with the correct one above
A  book falls off the top of a
book falls off the top of a  bookshelf. What is its final velocity right before it hits the ground?
bookshelf. What is its final velocity right before it hits the ground?

A 

The relationship between velocity and energy is:

We know the mass, but we need to find the total kinetic energy.
Remember the law of conservation of energy: the total energy at the beginning equals the total energy at the end. In this case, we have only potential energy at the beginning and only kinetic energy at the end. (The initial velocity is zero, and the final height is zero).

If we can find the potential energy, we can find the kinetic energy. The formula for potential energy is  .
.
Using our given values for the mass, height, and gravity, we can solve using multiplication. Note that the height becomes negative because the book is traveling in the downward direction.


The kinetic energy will also equal  , due to conservation of energy.
, due to conservation of energy.
Using this value and our given mass, we can calculate the velocity from our original kinetic energy equation.






Since we are taking the square root, our answer can be either negative or positive. The final velocity of the book will be in the downward direction; thus, our final velocity should be negative.

The relationship between velocity and energy is:
We know the mass, but we need to find the total kinetic energy.
Remember the law of conservation of energy: the total energy at the beginning equals the total energy at the end. In this case, we have only potential energy at the beginning and only kinetic energy at the end. (The initial velocity is zero, and the final height is zero).
If we can find the potential energy, we can find the kinetic energy. The formula for potential energy is 
Using our given values for the mass, height, and gravity, we can solve using multiplication. Note that the height becomes negative because the book is traveling in the downward direction.
The kinetic energy will also equal 
Using this value and our given mass, we can calculate the velocity from our original kinetic energy equation.
Since we are taking the square root, our answer can be either negative or positive. The final velocity of the book will be in the downward direction; thus, our final velocity should be negative.
Compare your answer with the correct one above
A baseball has a mass of  . If a high school pitcher can throw a baseball at
. If a high school pitcher can throw a baseball at  , what is the approximate kinetic energy associated with this pitch?
, what is the approximate kinetic energy associated with this pitch?
A baseball has a mass of 

To solve for the kinetic energy, we will need to use the equation:

Before we can plug in our given values, we must convert the mass from grams to kilograms. Remember, the SI unit for mass is kilograms, so most calculations will require this conversion.

Now we can use this mass and the given velocity to solve for the kinetic energy.



To solve for the kinetic energy, we will need to use the equation:
Before we can plug in our given values, we must convert the mass from grams to kilograms. Remember, the SI unit for mass is kilograms, so most calculations will require this conversion.
Now we can use this mass and the given velocity to solve for the kinetic energy.
Compare your answer with the correct one above
An orange falls off of a tree  tall. What is the final velocity of the orange before it hits the ground?
tall. What is the final velocity of the orange before it hits the ground?

An orange falls off of a tree 
For this problem, we need to use the law of conservation of energy. Since we are only looking at gravitational energy here and the orange starts at rest, we can say that the initial potential energy is equal to the final kinetic energy.
 .
.
From here, we can expand the equation, using the formulas for gravitational potential energy and kinetic energy.

Notice that the mass cancels out form both sides.

For the height, make sure to keep that value negative as we are measuring the DISPLACEMENT rather than the distance travelled. Since displacement is a vector (magnitude and direction) we need to be clear that it travels down  .
.





At this point, we need to remember that the square root of a positive number can be either positive or negative. Our velocity is a vector, so we will need to make sure we pick the answer choice with the appropriate direction. Since the orange is traveling downward, we know our final velocity must be negative.

For this problem, we need to use the law of conservation of energy. Since we are only looking at gravitational energy here and the orange starts at rest, we can say that the initial potential energy is equal to the final kinetic energy.

From here, we can expand the equation, using the formulas for gravitational potential energy and kinetic energy.
Notice that the mass cancels out form both sides.
For the height, make sure to keep that value negative as we are measuring the DISPLACEMENT rather than the distance travelled. Since displacement is a vector (magnitude and direction) we need to be clear that it travels down 
At this point, we need to remember that the square root of a positive number can be either positive or negative. Our velocity is a vector, so we will need to make sure we pick the answer choice with the appropriate direction. Since the orange is traveling downward, we know our final velocity must be negative.
Compare your answer with the correct one above