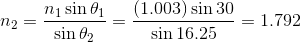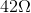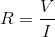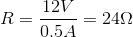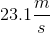College Physics

Help Questions

Physics › College Physics

Questions 1 - 10

A bowling ball is dropped from a height of onto a spring. If the spring is to compressed before halting the ball, what is the spring constant of the spring?

$588 \frac{N}{m}$

$2.35\times10^3 \frac{N}{m}$

$1.18\times10^3 \frac{N}{m}$

$294 \frac{N}{m^2}$

$34.3 \frac{N}{m}$

Explanation

This questions requires an understanding of the conversion of gravitational potential energy to potential energy stored in the compression of a spring. The ball's initial potential energy is where is the mass of the ball, is the acceleration due to gravity, and is the height of the ball. The energy stored in a compressed spring is $E = \frac{1}{2}kx^2$ where is the potential energy, is the spring constant (typically given in $\frac{N}{m}$ ) and is the compression of the spring. By setting the gravitational potential energy equal to the energy stored in the spring, we can solve for the spring constant :

$mgh=\frac{1}{2}kx^2$

$(12kg)(9.8\frac{m}{s^2})(10m)=\frac{1}{2}k(2m)^2$

$k=588 \frac{N}{m}$

A light ray is traveling through air hits a transparent material at an angle of from the normal. It is then refracted at . What is the speed of light in the material?

$1.7 \times 10^{8} \frac{m}{s}$

$2.2 \times 10^8 \frac{m}{s}$

$3.1 \times 10^8 \frac{m}{s}$

$1.3 \times 10^8 \frac{m}{s}$

Explanation

This problem requires Snell's Law and the corresponding equation:

$n_1\sin\theta_1 = n_2\sin\theta_2$

We know that the index of refraction of air is:

$n_1 = n_{air} = 1.0003$

We also know that:

$\theta_1 = 30$ and $\theta_2 = 16.25$

Now we can plug in these values into the Snell's Law equation to find the index of refraction for the transparent material.

$n_2 = \frac{n_1\sin\theta_1}{\sin\theta_2} = \frac{(1.003)\sin30}{\sin16.25} = 1.792$

Finally, we need to calculate the speed of light moving through this transparent material now that we know the index of refraction for it. To do that, we need to use this equation:

$V = \frac{c}{n}$

Where is the speed of light and is the index of refraction. We plug in our known values and get:

$V = \frac{c}{n} = \frac{3.0\times10^8}{1.792}= 1.7\times10^8\frac{m}{s}$

You are given three resistors with known values:

$R1=100\Omega$

$R2=50\Omega$

$R3=10\Omega$

You are asked to create a circuit with a total resistance of between $40\Omega$ and $45\Omega$ . How should you arrange the resistors to accomplish this?

and in parallel, connected to in series

, , and in parallel

and in parallel, connected to in series

and in parallel; is not necessary

, , and in series

Explanation

This question requires no math to correctly answer! You should not need to 'brute force' it. Although it is designed to appear time consuming, it should be relatively easily once the principle of resistors in parallel is understood. Whenever two resistors are connected in parallel, the net resistance must be less than the resistance of either of the two alone. When resistors are connected in series, the net resistance must be more than the resistance of either alone.

Explanation of correct answer:

and in parallel, connected to in series - It is possible to 'eyeball' this to see that this is at least feasible. and in parallel must make a network with an overall resistance less than $50\Omega$ . When added in series with ( $10\Omega$ ), the overall may fall between $40\Omega$ and $45\Omega$ . To confirm, one could do the math to calculate the overall resistance, but the point of this question is to use general principles to quickly eliminate the other, incorrect answer choices.

Explanations of incorrect answers:

, , and in parallel - This combination cannot possibly work since the overall resistance must be less than $10\Omega$ (the smallest resistor in parallel).

and in parallel, connected to in series - Regardless of the overall resistance of and in parallel, the connection with in series makes the total resistance more than $100\Omega$ .

and in parallel; is not necessary - Placing and in parallel must result in a resistance less than $10\Omega$ .

, , and in series - Connecting resistors in series results in an overall resistance greater than that of any one alone. Since and are included in series, the sum of the resistances is obviously much greater than what we are asked to produce and this choice can be immediately eliminated.

Suppose that the fifth harmonic of a standing wave contained within a pipe closed at both ends has a wavelength of . What is the length of the pipe?

Explanation

For this question, we're told that a standing wave is contained within a pipe closed at both ends. We're also given the wavelength for the fifth harmonic, and are asked to find the length of the pipe.

The first step to solve this problem is to use the equation for a pipe closed at both ends.

$L=n\frac{\lambda}{2}$

Since we're told which harmonic the wave is on, as well as its wavelength, we have everything we need to solve for the length of the pipe.

$L=5(\frac{420:cm}{2})=1050:cm$

What is the RMS voltage of a peak-to-peak AC current?

Explanation

This question requires two steps: the first is to calculate the peak voltage of the AC current, and the second requires conversion of the peak voltage to an RMS voltage. We are told that the current is peak-to-peak. Thus, the peak voltage is half of this, or . By definition, to convert peak voltage to RMS voltage, we must divide the peak voltage by $\sqrt{2}$ :

$\frac{50V}{\sqrt{2}} = 35.5V$

What size resistor should be connected across the terminals of a battery to produce a current of ?

$24\Omega$

$6\Omega$

$42\Omega$

$0.042\Omega$

$24k\Omega$

Explanation

Ohm's law is .

In this case, and .

Solving for the resistance, , we get:

$R=\frac{V}{I}$

Substitute known values and solve for the unknown resistance:

$R=\frac{12V}{0.5A}=24\Omega$

An hourglass is placed on a scale with all its sand in the upper chamber. A short time later, the sand begins to fall into the lower chamber. Which of the following best describes the reading on the scale as a function of time before any sand has accumulated in the bottom chamber?

The reading on the scale decreases slightly.

The reading on the scale stays the same.

None of these

The reading on the scale increases.

The reading on the scale is zero.

Explanation

Initially, when all the sand is in the upper chamber, the reading on the scale is constant and corresponds to the weight of the hourglass and the sand within. As some sand falls, there is no normal force on it so the scale can not register its weight. The fraction of sand that is falling is small, so there is only a small decrease in the apparent weight of the hourglass.

A baseball has a mass of , but it weighs when completely submerged in water. What is its volume assuming that the density of water is $1000 \frac{kg}{m^3}$ ?

$2.09\times 10^{5} cm^{3}$

Explanation

We are given the mass of the baseball outside of the water. Using the weight equation with the gravitational constant being $9.8\frac{m}{s^2}$ and the mass being , the weight of the baseball outside of the water is 4.905 N. (Be careful and convert the mass of the baseball from grams to kilograms since we are using SI units).

The buoyancy force is the difference of the weight of the baseball when it is in the air and when it is in the water. So subtract the two differences:

Now we use the buoyancy equation:

$B = \rho Vg$ where is the buoyancy force, $\rho$ is the density of water, is the volume of the baseball, and is the gravitational constant. Plug in the known variables and solve for the volume.

$0.205N = (1000\frac{kg}{m^3}) V (9.81\frac{m}{s^2})$

and we get $V = 2.09\times 10^{-5}m^3 = 20.9 cm^3$

Consider the image shown below.

Pressure difference

In the container on the left, there is a gas at an unknown pressure. The tubing connected to the container is open to the atmosphere, which has a pressure of . If the liquid contained within the tubing shows a pressure difference of , as in the above image, what is the pressure of the gas in the container?

Explanation

In this question, we're told that an unknown gas is held within a container. Connected to this container is a tube open to the atmosphere which also contains a liquid. Based on the image shown, the height difference of the liquid levels, and the atmospheric pressure, we're asked to determine the pressure of the unknown gas inside the container.

This is a fairly straight-forward problem that asks us about pressure. Because of the way the tubing is situated, the pressure from the atmosphere will push down on the right side of the tubing, while the pressure from the unknown gas in the container will push down on the left part of the tubing. Since the liquid level on the left is lower than on the right, we can infer that the gas in the container is "pushing" on the liquid more strongly than the atmosphere on the other side. Consequently, we know that the gas in the container has a pressure greater than atmospheric pressure.

The difference in height of the liquid levels allows us to quantitatively determine how much greater this pressure is. Since the height difference shows up as , we know that the gas in the container is more than atmospheric pressure.

Fluid flows into a pipe with a diameter of at a rate of $5\frac{m}{s}$ . If the other end of the pipe has a cross sectional area of , what is the speed of the fluid as it exits the pipe?

$31.4\frac{m}{s}$

$23.1\frac{m}{s}$

$17\frac{m}{s}$

$1.3\frac{m}{s}$

$5\frac{m}{s}$

Explanation

This question tests the concept of the continuity equation which stipulates that at steady state the volume flowing into one end of a pipe must be exactly equal to the volume flowing out of the other end. That is, . Note that in this case, we are given the inlet diameter and not cross-sectional area. Thus, we must also find the inlet's cross-sectional area by using the formula for the area of a circle.

$(\pi)(2\frac{m}{s})^2(5\frac{m}{s}) = (0.5m^2)V_2$

$V_2=31.4 \frac{m}{s}$

Page 1 of 50

Return to subject