How to find the length of an edge of a tetrahedron - PSAT Math
Card 1 of 7
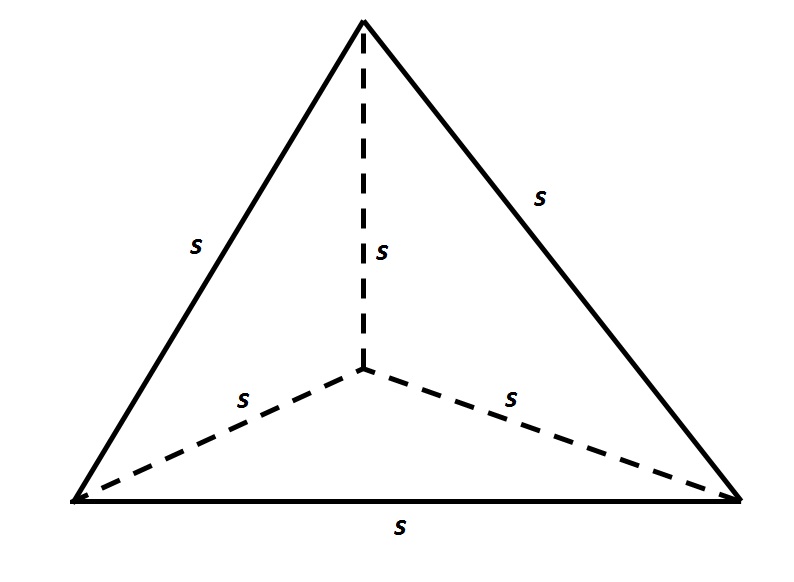
Refer to the above tetrahedron, or four-faced solid.The surface area of the tetrahedron is 444. Evaluate  to the nearest tenth.
to the nearest tenth.

Refer to the above tetrahedron, or four-faced solid.The surface area of the tetrahedron is 444. Evaluate 
Tap to reveal answer
The tetrahedron has four faces, each of which is an equilateral triangle with sidelength  . Since the total surface area is 444, each triangle has area one fourth of this, or 111. To find
. Since the total surface area is 444, each triangle has area one fourth of this, or 111. To find  , set
, set 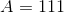 in the formula for the area of an equilateral triangle:
in the formula for the area of an equilateral triangle:
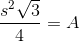

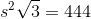


The tetrahedron has four faces, each of which is an equilateral triangle with sidelength 

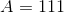
← Didn't Know|Knew It →

Refer to the above tetrahedron, or four-faced solid.The surface area of the tetrahedron is 444. Evaluate  to the nearest tenth.
to the nearest tenth.

Refer to the above tetrahedron, or four-faced solid.The surface area of the tetrahedron is 444. Evaluate 
Tap to reveal answer
The tetrahedron has four faces, each of which is an equilateral triangle with sidelength  . Since the total surface area is 444, each triangle has area one fourth of this, or 111. To find
. Since the total surface area is 444, each triangle has area one fourth of this, or 111. To find  , set
, set 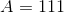 in the formula for the area of an equilateral triangle:
in the formula for the area of an equilateral triangle:
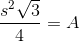

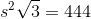


The tetrahedron has four faces, each of which is an equilateral triangle with sidelength 

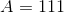
← Didn't Know|Knew It →

Refer to the above tetrahedron, or four-faced solid.The surface area of the tetrahedron is 444. Evaluate  to the nearest tenth.
to the nearest tenth.

Refer to the above tetrahedron, or four-faced solid.The surface area of the tetrahedron is 444. Evaluate 
Tap to reveal answer
The tetrahedron has four faces, each of which is an equilateral triangle with sidelength  . Since the total surface area is 444, each triangle has area one fourth of this, or 111. To find
. Since the total surface area is 444, each triangle has area one fourth of this, or 111. To find  , set
, set  in the formula for the area of an equilateral triangle:
in the formula for the area of an equilateral triangle:
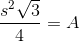

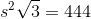


The tetrahedron has four faces, each of which is an equilateral triangle with sidelength 

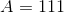
← Didn't Know|Knew It →

Refer to the above tetrahedron, or four-faced solid.The surface area of the tetrahedron is 444. Evaluate  to the nearest tenth.
to the nearest tenth.

Refer to the above tetrahedron, or four-faced solid.The surface area of the tetrahedron is 444. Evaluate 
Tap to reveal answer
The tetrahedron has four faces, each of which is an equilateral triangle with sidelength  . Since the total surface area is 444, each triangle has area one fourth of this, or 111. To find
. Since the total surface area is 444, each triangle has area one fourth of this, or 111. To find  , set
, set 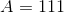 in the formula for the area of an equilateral triangle:
in the formula for the area of an equilateral triangle:
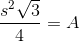

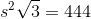


The tetrahedron has four faces, each of which is an equilateral triangle with sidelength 

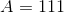
← Didn't Know|Knew It →

Refer to the above tetrahedron, or four-faced solid.The surface area of the tetrahedron is 444. Evaluate  to the nearest tenth.
to the nearest tenth.

Refer to the above tetrahedron, or four-faced solid.The surface area of the tetrahedron is 444. Evaluate 
Tap to reveal answer
The tetrahedron has four faces, each of which is an equilateral triangle with sidelength  . Since the total surface area is 444, each triangle has area one fourth of this, or 111. To find
. Since the total surface area is 444, each triangle has area one fourth of this, or 111. To find  , set
, set 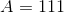 in the formula for the area of an equilateral triangle:
in the formula for the area of an equilateral triangle:
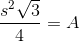

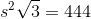


The tetrahedron has four faces, each of which is an equilateral triangle with sidelength 

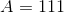
← Didn't Know|Knew It →

Refer to the above tetrahedron, or four-faced solid.The surface area of the tetrahedron is 444. Evaluate  to the nearest tenth.
to the nearest tenth.

Refer to the above tetrahedron, or four-faced solid.The surface area of the tetrahedron is 444. Evaluate 
Tap to reveal answer
The tetrahedron has four faces, each of which is an equilateral triangle with sidelength  . Since the total surface area is 444, each triangle has area one fourth of this, or 111. To find
. Since the total surface area is 444, each triangle has area one fourth of this, or 111. To find  , set
, set 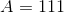 in the formula for the area of an equilateral triangle:
in the formula for the area of an equilateral triangle:
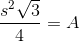

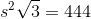


The tetrahedron has four faces, each of which is an equilateral triangle with sidelength 

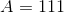
← Didn't Know|Knew It →

Refer to the above tetrahedron, or four-faced solid.The surface area of the tetrahedron is 444. Evaluate  to the nearest tenth.
to the nearest tenth.

Refer to the above tetrahedron, or four-faced solid.The surface area of the tetrahedron is 444. Evaluate 
Tap to reveal answer
The tetrahedron has four faces, each of which is an equilateral triangle with sidelength  . Since the total surface area is 444, each triangle has area one fourth of this, or 111. To find
. Since the total surface area is 444, each triangle has area one fourth of this, or 111. To find  , set
, set 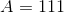 in the formula for the area of an equilateral triangle:
in the formula for the area of an equilateral triangle:
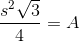

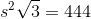


The tetrahedron has four faces, each of which is an equilateral triangle with sidelength 

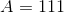
← Didn't Know|Knew It →