Venn Diagrams - SAT Math
Card 0 of 203
Doug has a cow farm. Some of Doug's cows are used for milk, some are used for reproduction and some are used for both. If he has a total of 40 cows and 10 are used only for milk and 3 are used for both milk and reproduction, then how many cows are used for reproduction?
Doug has a cow farm. Some of Doug's cows are used for milk, some are used for reproduction and some are used for both. If he has a total of 40 cows and 10 are used only for milk and 3 are used for both milk and reproduction, then how many cows are used for reproduction?
Since we know that only 10 cows are for milk only we must subtract this number from the total amount of cows to get our answer: 40 – 10 = 30 cows. The cows that do both are still used for reproduction, so the correct answer is 30 cows.
Since we know that only 10 cows are for milk only we must subtract this number from the total amount of cows to get our answer: 40 – 10 = 30 cows. The cows that do both are still used for reproduction, so the correct answer is 30 cows.
Compare your answer with the correct one above
All students have to take at least one math class and one language class. Twenty students take calculus, and thirty students take statistics. Fifteen students take Spanish and twenty-five take French. If there are thirty-five students total, what is the maximum number of students taking both two math classes and two language classes.
All students have to take at least one math class and one language class. Twenty students take calculus, and thirty students take statistics. Fifteen students take Spanish and twenty-five take French. If there are thirty-five students total, what is the maximum number of students taking both two math classes and two language classes.
Totalling the number in math there are 50 students on the rosters of all the math classes. With 35 total students this means that there are 15 students taking 2 math classes. For the language classes there are 40 students on the roster, showing that 5 students are taking 2 language classes. The maximum number of students taking two math classes and two language classes is only as great as the smallest number taking a double math or language class, which is 5 students (limited by the language doubles).
Totalling the number in math there are 50 students on the rosters of all the math classes. With 35 total students this means that there are 15 students taking 2 math classes. For the language classes there are 40 students on the roster, showing that 5 students are taking 2 language classes. The maximum number of students taking two math classes and two language classes is only as great as the smallest number taking a double math or language class, which is 5 students (limited by the language doubles).
Compare your answer with the correct one above
At a certain college, some members of the baseball team are seniors and all seniors are in statistics class. Which statement is must be true?
At a certain college, some members of the baseball team are seniors and all seniors are in statistics class. Which statement is must be true?
The statement says all seniors take statistics so if you are a senior you are in statistics automatically. It also said some baseball team members are seniors which means at least some teammates must be in statistics.
The statement says all seniors take statistics so if you are a senior you are in statistics automatically. It also said some baseball team members are seniors which means at least some teammates must be in statistics.
Compare your answer with the correct one above
In a group of 83 gym members, 51 are taking kickboxing and 25 are taking yoga. Of the students taking kickboxing or yoga, 11 are taking both classes. How many members are not taking either course?
In a group of 83 gym members, 51 are taking kickboxing and 25 are taking yoga. Of the students taking kickboxing or yoga, 11 are taking both classes. How many members are not taking either course?
If 11 people are taking both courses, this means 51-11 or 40 are taking kickboxing only and 25-11 or 14 are taking yoga only. The number of people taking at least one course, therefore, is 40 + 14 + 11 = 65. The 83 members minus the 65 that are taking courses leaves 18 who are not taking any courses.
If 11 people are taking both courses, this means 51-11 or 40 are taking kickboxing only and 25-11 or 14 are taking yoga only. The number of people taking at least one course, therefore, is 40 + 14 + 11 = 65. The 83 members minus the 65 that are taking courses leaves 18 who are not taking any courses.
Compare your answer with the correct one above
In a school of 1250 students, 50% of the students take an art class and 50% of the students take a gym class. If 450 students take neither art nor gym class, then how many students take both art and gym?
In a school of 1250 students, 50% of the students take an art class and 50% of the students take a gym class. If 450 students take neither art nor gym class, then how many students take both art and gym?
You can construct a Venn diagran in which one circle represents art (A), the other represents gym (B), the region of overlap is designated (C), and the number of students not present in either circle is designated (S).
First, it is given that S=450.
50% of students take art and 50% take gym and the total number of students is 1250. 50% of 1250 is 625. Thus, A+C=625 and B+C=625.
Setting them equal to each other we get A+C=B+C.
Subtract C from both sides to get A=B; so the same number of students take art only and gym only.
Now 1250-450= A+B+C=800.
Since A=B we can use substitution to get 2A+C=800.
Finally you can solve the system of equations using the method of your choice (substitution or elimination) to solve the system with A+C=625 and 2A+C=800.
For substitution, we solve for C in the first equation to get C=625-A. Then we substitute this value into the second equation to get 2A+ (625-A)=800. Solve for A to get A=175, so B=175 also. Since A+B+C = 800, C=450.
You can construct a Venn diagran in which one circle represents art (A), the other represents gym (B), the region of overlap is designated (C), and the number of students not present in either circle is designated (S).
First, it is given that S=450.
50% of students take art and 50% take gym and the total number of students is 1250. 50% of 1250 is 625. Thus, A+C=625 and B+C=625.
Setting them equal to each other we get A+C=B+C.
Subtract C from both sides to get A=B; so the same number of students take art only and gym only.
Now 1250-450= A+B+C=800.
Since A=B we can use substitution to get 2A+C=800.
Finally you can solve the system of equations using the method of your choice (substitution or elimination) to solve the system with A+C=625 and 2A+C=800.
For substitution, we solve for C in the first equation to get C=625-A. Then we substitute this value into the second equation to get 2A+ (625-A)=800. Solve for A to get A=175, so B=175 also. Since A+B+C = 800, C=450.
Compare your answer with the correct one above
Sets P, Q, and R consist of the positive factors of 48, 90, and 56, respectively. If set T = P U (Q ∩ R), which of the following does NOT belong to T?
Sets P, Q, and R consist of the positive factors of 48, 90, and 56, respectively. If set T = P U (Q ∩ R), which of the following does NOT belong to T?
First, let's find the factors of 48, which will give us all of the elements in P. In order to find the factors of 48, list the pairs of numbers whose product is 48.
The pairs are as follows:
1 and 48; 2 and 24; 3 and 16; 4 and 12; 6 and 8
Therefore the factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48.
Now we can write P = {1, 2, 3, 4, 6, 8, 12, 16, 24, 48}.
Next, we need to find the factors of 90.
Again list the pairs:
1 and 90; 2 and 45; 3 and 30; 5 and 18; 6 and 15; 9 and 10
Then the factors of 90 are 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, and 90.
Thus, Q = {1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90}.
Next find the factors of 56:
1 and 56; 2 and 28; 4 and 14; 7 and 8
Set R = {1, 2, 4, 7, 8, 14, 28, 56}
Now, we need to find set T, which is P U (Q ∩ R).
We have to start inside the parantheses with Q ∩ R. The intersection of two sets consists of all of the elements that the two sets have in common. The only elements that Q and R have in common are 1 and 2.
Q ∩ R = {1, 2}
Lastly, we must find P U (Q ∩ R).
The union of two sets consists of any element that is in either of the two sets. Thus, the union of P and Q ∩ R will consist of the elements that are either in P or in Q ∩ R. The following elements are in either P or Q ∩ R:
{1, 2, 3, 4, 6, 8, 12, 16, 24, 48}
Therefore, T = {1, 2, 3, 4, 6, 8, 12, 16, 24, 48}.
The problem asks us to determine which choice does NOT belong to T. The number 28 doesn't belong to T.
The answer is 28.
First, let's find the factors of 48, which will give us all of the elements in P. In order to find the factors of 48, list the pairs of numbers whose product is 48.
The pairs are as follows:
1 and 48; 2 and 24; 3 and 16; 4 and 12; 6 and 8
Therefore the factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48.
Now we can write P = {1, 2, 3, 4, 6, 8, 12, 16, 24, 48}.
Next, we need to find the factors of 90.
Again list the pairs:
1 and 90; 2 and 45; 3 and 30; 5 and 18; 6 and 15; 9 and 10
Then the factors of 90 are 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, and 90.
Thus, Q = {1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90}.
Next find the factors of 56:
1 and 56; 2 and 28; 4 and 14; 7 and 8
Set R = {1, 2, 4, 7, 8, 14, 28, 56}
Now, we need to find set T, which is P U (Q ∩ R).
We have to start inside the parantheses with Q ∩ R. The intersection of two sets consists of all of the elements that the two sets have in common. The only elements that Q and R have in common are 1 and 2.
Q ∩ R = {1, 2}
Lastly, we must find P U (Q ∩ R).
The union of two sets consists of any element that is in either of the two sets. Thus, the union of P and Q ∩ R will consist of the elements that are either in P or in Q ∩ R. The following elements are in either P or Q ∩ R:
{1, 2, 3, 4, 6, 8, 12, 16, 24, 48}
Therefore, T = {1, 2, 3, 4, 6, 8, 12, 16, 24, 48}.
The problem asks us to determine which choice does NOT belong to T. The number 28 doesn't belong to T.
The answer is 28.
Compare your answer with the correct one above
The class of 2034 at Make Believe High School graduated 50 students. 13 students studied only math. 35 students studied English. 30 students studied only 2 subjects. Only 4 students studied writing, it was the third subject for all of them. How many students did not study anything?
The class of 2034 at Make Believe High School graduated 50 students. 13 students studied only math. 35 students studied English. 30 students studied only 2 subjects. Only 4 students studied writing, it was the third subject for all of them. How many students did not study anything?
The answer is 2. Taking away the 4 writing students, the 13 math-only students, and the remaining 31 English students, we have 2 students remaining.
The answer is 2. Taking away the 4 writing students, the 13 math-only students, and the remaining 31 English students, we have 2 students remaining.
Compare your answer with the correct one above
The universal set is positive counting numbers less than 11. Set A = {1, 3, 5} and Set B = { 2, 4, 6}.
What is 
?
The universal set is positive counting numbers less than 11. Set A = {1, 3, 5} and Set B = { 2, 4, 6}.
What is
means intersection and 
means union
U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {1, 3, 5}
A' = {2, 4, 6, 7, 8, 9, 10}
B = {2, 4, 6}
B' = {1, 3, 5, 7, 8, 9, 10}
= {2, 4, 6}
= {1, 3, 5}
= {1, 2, 3, 4, 5, 6}
U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {1, 3, 5}
A' = {2, 4, 6, 7, 8, 9, 10}
B = {2, 4, 6}
B' = {1, 3, 5, 7, 8, 9, 10}
Compare your answer with the correct one above
Sixty high school seniors were polled to see if they were taking history and calculus. A total of 29 students said they were taking calculus, and a total of 50 students said they were taking history. What is the minimum number of students who take both history and calculus?
Sixty high school seniors were polled to see if they were taking history and calculus. A total of 29 students said they were taking calculus, and a total of 50 students said they were taking history. What is the minimum number of students who take both history and calculus?
We can draw a Venn diagram to see these two sets of students.
We need to find the overlap between these two sets. To find that, add up the total number of students who are taking history and the total number of students who are taking calculus.
Notice that we have more students this way than the total number who were polled. That is because the students who are taking history AND calculus have been double counted. Subtract the total number of students polled to find out how many students were counted twice.
We can draw a Venn diagram to see these two sets of students.
We need to find the overlap between these two sets. To find that, add up the total number of students who are taking history and the total number of students who are taking calculus.
Notice that we have more students this way than the total number who were polled. That is because the students who are taking history AND calculus have been double counted. Subtract the total number of students polled to find out how many students were counted twice.
Compare your answer with the correct one above
Given the Venn diagram below, which of the following does not belong to 
?
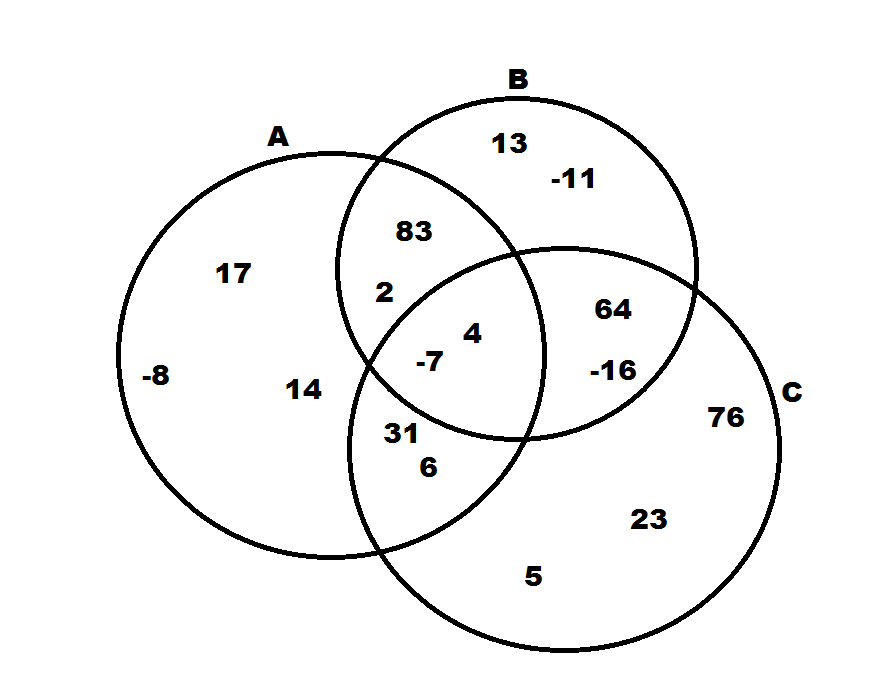
Given the Venn diagram below, which of the following does not belong to
The symbol 
stands for the union between two sets. Therefore, 
means the set of all numbers that are in either A or B. Looking at our choices, the only number that isn't in either A, B, or both is 23.
The symbol
Compare your answer with the correct one above
Forty students play soccer and/or basketball after school. Twenty-four students play soccer and twenty-nine play basketball. How many students play both soccer and basketball?
Forty students play soccer and/or basketball after school. Twenty-four students play soccer and twenty-nine play basketball. How many students play both soccer and basketball?
We can draw a Venn diagram of these students.
Drawn this way, there are more students on the Venn diagram than we have.
This is because some of the students play both sports and should be in the overlap on the Venn diagram. To find the number of students in the overlap, subtract the total number of students given from the number on the diagram.
This represents the number of students who were counted twice, or the number in the overlap.
We can redraw the correct Venn diagram with this number.
We can draw a Venn diagram of these students.
Drawn this way, there are more students on the Venn diagram than we have.
This is because some of the students play both sports and should be in the overlap on the Venn diagram. To find the number of students in the overlap, subtract the total number of students given from the number on the diagram.
This represents the number of students who were counted twice, or the number in the overlap.
We can redraw the correct Venn diagram with this number.
Compare your answer with the correct one above
Giving the Venn diagram above, what is the sum of the numbers in the set 
?
Giving the Venn diagram above, what is the sum of the numbers in the set
The notation 
stands for "A union C," which refers to everything that is in either set 
or set 
.
When we add the numbers together, we get:
The notation
When we add the numbers together, we get:
Compare your answer with the correct one above
A group of high school juniors are taking Biology, Calculus, and Spanish as shown above. Which student is not in the set 
?
A group of high school juniors are taking Biology, Calculus, and Spanish as shown above. Which student is not in the set
The notation 
stands for "union," which refers to everything that is in either set. 
refers to the group of students taking either Calculus or Spanish (everyone on this diagram except those taking only Biology). From the diagram, Patrick and Ashley are the only students taking neither Calculus nor Spanish, so Patrick is the correct answer.
The notation
Compare your answer with the correct one above
In a class of senior high-school students, 
have pet cats, 
have pet dogs, 
have both cats and dogs, and 
have neither cats nor dogs. How many total students are in the class?
In a class of senior high-school students,
A Venn diagram can help us determine the total number of students in the class.
First, we must calculate the number of students who have ONLY cats or ONLY dogs. First, for cats, 15 students have cats, and 5 students have both cats and dogs.
Ten students have only cats.
For dogs, 12 students have dogs, and 5 students have both cats and dogs.
Seven students have only dogs.
Using this information, we can fill in the Venn diagram.
This diagram shows the 10 students with only cats, the 7 students with only dogs, the 5 students with both, and the 8 students with neither. Adding up the numbers will give us the total number of students.
A Venn diagram can help us determine the total number of students in the class.
First, we must calculate the number of students who have ONLY cats or ONLY dogs. First, for cats, 15 students have cats, and 5 students have both cats and dogs.
Ten students have only cats.
For dogs, 12 students have dogs, and 5 students have both cats and dogs.
Seven students have only dogs.
Using this information, we can fill in the Venn diagram.
This diagram shows the 10 students with only cats, the 7 students with only dogs, the 5 students with both, and the 8 students with neither. Adding up the numbers will give us the total number of students.
Compare your answer with the correct one above
Farmer John has one hundred plots of land. Sixty plots grow corn. Forty plots grow carrots. These numbers take into account that some of the plots grow both corn and carrots.
How many plots grow both corn and carrots?
Farmer John has one hundred plots of land. Sixty plots grow corn. Forty plots grow carrots. These numbers take into account that some of the plots grow both corn and carrots.
How many plots grow both corn and carrots?
To find how many plots grow both carrots and corn, we subtract 
.
That means that fifty plots grow corn only, while thirty plots grow carrots only.
To find how many plots grow both carrots and corn, we subtract
That means that fifty plots grow corn only, while thirty plots grow carrots only.
Compare your answer with the correct one above
Let Set A = 
and Set B = 
.
What is 
?
Let Set A =
What is
represents the union of the two sets. The union of Sets A and B is the set of elements which appear in A, in B, or in both A and B.
Therefore, 
Therefore,
Compare your answer with the correct one above
Fifty 6th graders were asked what their favorite school subjects were. Three students like math, science and English. Five students liked math and science. Seven students liked math and English. Eight people liked science and English. Twenty students liked science. Twenty-eight students liked English. Fourteen students liked math. How many students didn’t like any of these classes?
Fifty 6th graders were asked what their favorite school subjects were. Three students like math, science and English. Five students liked math and science. Seven students liked math and English. Eight people liked science and English. Twenty students liked science. Twenty-eight students liked English. Fourteen students liked math. How many students didn’t like any of these classes?
Draw a Venn diagram with three subsets: Math, Science, and English. Start in the center with students that like all three subjects. Next, look at students that liked two subjects. Be sure to subtract out the ones already counted in the middle. Then, look at the students that only like one subject. Be sure to subtract out the students already accounted for. Once all of the subsets are filled, look at those students who don’t like any of these subjects. To find the students who don’t like any of these subjects add all of the students who like at least one subject from the total number of students surveyed, which is 50.
M = math
S = science
E = English
M∩S∩E = 3
M∩S = 5 (but 3 are already accounted for) so 2 for M and S ONLY
M∩E = 7 (but 3 are already accounted for) so 4 for M and E ONLY
S∩E = 8 (but 3 are already accounted for) so 5 for S and E ONLY
M = 14 (but 3 + 2 + 4 are already accounted for) so 5 for M ONLY
S = 20 (but 3 + 2 + 5 are already accounted for) so 10 for S ONLY
E = 28 (but 3 + 4 + 5 are already accounted for) so 16 for E ONLY
Therefore, the students already accounted for is 3 + 2 +4 + 5 + 5 + 10 + 16 = 45 students
So, those students who don’t like any of these subjects are 50 – 45 = 5 students
Draw a Venn diagram with three subsets: Math, Science, and English. Start in the center with students that like all three subjects. Next, look at students that liked two subjects. Be sure to subtract out the ones already counted in the middle. Then, look at the students that only like one subject. Be sure to subtract out the students already accounted for. Once all of the subsets are filled, look at those students who don’t like any of these subjects. To find the students who don’t like any of these subjects add all of the students who like at least one subject from the total number of students surveyed, which is 50.
M = math
S = science
E = English
M∩S∩E = 3
M∩S = 5 (but 3 are already accounted for) so 2 for M and S ONLY
M∩E = 7 (but 3 are already accounted for) so 4 for M and E ONLY
S∩E = 8 (but 3 are already accounted for) so 5 for S and E ONLY
M = 14 (but 3 + 2 + 4 are already accounted for) so 5 for M ONLY
S = 20 (but 3 + 2 + 5 are already accounted for) so 10 for S ONLY
E = 28 (but 3 + 4 + 5 are already accounted for) so 16 for E ONLY
Therefore, the students already accounted for is 3 + 2 +4 + 5 + 5 + 10 + 16 = 45 students
So, those students who don’t like any of these subjects are 50 – 45 = 5 students
Compare your answer with the correct one above
Set A contains the positive even integers less than 14. Set B contains the positive multiples of three less than 20. What is the intersection of the two sets?
Set A contains the positive even integers less than 14. Set B contains the positive multiples of three less than 20. What is the intersection of the two sets?
A = {2, 4, 6, 8, 10, 12}
B = {3, 6, 9, 12, 15, 18}
The intersection of a set means that the elements are in both sets: A∩B = {6, 12}
A = {2, 4, 6, 8, 10, 12}
B = {3, 6, 9, 12, 15, 18}
The intersection of a set means that the elements are in both sets: A∩B = {6, 12}
Compare your answer with the correct one above
There are 75 juniors at a high school. 15 of the students are enrolled in Physics and 40 students are enrolled in Chemistry. 30 students are not enrolled in either Physics or Chemistry. How many students are enrolled in both Physics and Chemistry?
There are 75 juniors at a high school. 15 of the students are enrolled in Physics and 40 students are enrolled in Chemistry. 30 students are not enrolled in either Physics or Chemistry. How many students are enrolled in both Physics and Chemistry?
First, subtract the students that are in neither class; 75 – 30 = 45 students.
Thus, 45 students are enrolled in Chemistry, Physics, or both. Of these 45 students, we know 40 are in Chemistry, so that leaves 5 students who are enrolled in Physics only; with 15 total students in Physics, that means 10 must be in Chemistry as well. So 10 students are in both Physics and Chemistry.
First, subtract the students that are in neither class; 75 – 30 = 45 students.
Thus, 45 students are enrolled in Chemistry, Physics, or both. Of these 45 students, we know 40 are in Chemistry, so that leaves 5 students who are enrolled in Physics only; with 15 total students in Physics, that means 10 must be in Chemistry as well. So 10 students are in both Physics and Chemistry.
Compare your answer with the correct one above
100 students are in the 10th grade class. 30 are swimmers, 40 are runners, and 20 are swimmers and runners. What is the probability that a student is a swimmer OR a runner?
100 students are in the 10th grade class. 30 are swimmers, 40 are runners, and 20 are swimmers and runners. What is the probability that a student is a swimmer OR a runner?
The formula for intersection is P(a or b) = P(a) + P(b) – P(a and b).
Now, 30 students out of 100 swim, so P(swim) = 30/100 = 3/10.
40 students run out of 100, so P(run) = 40/100 = 4/10. Notice how we are keeping 10 as the common denominator even though we could simplify this further. Keeping all of the fractions similar will make the addition and subtraction easier later on.
Finally, 20 students swim AND run, so P(swim AND run) = 20/100 = 2/10. (Again, we keep this as 2/10 instead of 1/5 so that we can combine the three fractions more easily.)
P(swim OR run) = P(swim) + P(run) – P(swim and run)
= 3/10 + 4/10 – 2/10 = 5/10 = 1/2.
The formula for intersection is P(a or b) = P(a) + P(b) – P(a and b).
Now, 30 students out of 100 swim, so P(swim) = 30/100 = 3/10.
40 students run out of 100, so P(run) = 40/100 = 4/10. Notice how we are keeping 10 as the common denominator even though we could simplify this further. Keeping all of the fractions similar will make the addition and subtraction easier later on.
Finally, 20 students swim AND run, so P(swim AND run) = 20/100 = 2/10. (Again, we keep this as 2/10 instead of 1/5 so that we can combine the three fractions more easily.)
P(swim OR run) = P(swim) + P(run) – P(swim and run)
= 3/10 + 4/10 – 2/10 = 5/10 = 1/2.
Compare your answer with the correct one above