Squaring / Square Roots / Radicals - SAT Math
Card 0 of 424
Simplify: 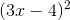
Simplify:
If you don't already have the pattern memorized, use FOIL. It's best to write out the parentheses twice (as below) to avoid mistakes:


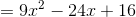
If you don't already have the pattern memorized, use FOIL. It's best to write out the parentheses twice (as below) to avoid mistakes:
Compare your answer with the correct one above
Simplify the radical.

Simplify the radical.
We can break the square root down into 2 roots of 67 and 49. 49 is a perfect square and reduces to 7.
We can break the square root down into 2 roots of 67 and 49. 49 is a perfect square and reduces to 7.
Compare your answer with the correct one above
Simplify: 
Simplify:
If you don't already have the pattern memorized, use FOIL. It's best to write out the parentheses twice (as below) to avoid mistakes:




If you don't already have the pattern memorized, use FOIL. It's best to write out the parentheses twice (as below) to avoid mistakes:
Compare your answer with the correct one above
x2 = 36
Quantity A: x
Quantity B: 6
x2 = 36
Quantity A: x
Quantity B: 6
x2 = 36 -> it is important to remember that this leads to two answers.
x = 6 or x = -6.
If x = 6: A = B.
If x = -6: A < B.
Thus the relationship cannot be determined from the information given.
x2 = 36 -> it is important to remember that this leads to two answers.
x = 6 or x = -6.
If x = 6: A = B.
If x = -6: A < B.
Thus the relationship cannot be determined from the information given.
Compare your answer with the correct one above
According to Heron's Formula, the area of a triangle with side lengths of a, b, and c is given by the following:

where s is one-half of the triangle's perimeter.
What is the area of a triangle with side lengths of 6, 10, and 12 units?
According to Heron's Formula, the area of a triangle with side lengths of a, b, and c is given by the following:
where s is one-half of the triangle's perimeter.
What is the area of a triangle with side lengths of 6, 10, and 12 units?
We can use Heron's formula to find the area of the triangle. We can let a = 6, b = 10, and c = 12.
In order to find s, we need to find one half of the perimeter. The perimeter is the sum of the lengths of the sides of the triangle.
Perimeter = a + b + c = 6 + 10 + 12 = 28
In order to find s, we must multiply the perimeter by one-half, which would give us (1/2)(28), or 14.
Now that we have a, b, c, and s, we can calculate the area using Heron's formula.


We can use Heron's formula to find the area of the triangle. We can let a = 6, b = 10, and c = 12.
In order to find s, we need to find one half of the perimeter. The perimeter is the sum of the lengths of the sides of the triangle.
Perimeter = a + b + c = 6 + 10 + 12 = 28
In order to find s, we must multiply the perimeter by one-half, which would give us (1/2)(28), or 14.
Now that we have a, b, c, and s, we can calculate the area using Heron's formula.
Compare your answer with the correct one above
Simplify the expression.

Simplify the expression.
Use the distributive property for radicals.

Multiply all terms by  .
.

Combine terms under radicals.


Look for perfect square factors under each radical.  has a perfect square of
has a perfect square of  . The
. The  can be factored out.
can be factored out.


Since both radicals are the same, we can add them.

Use the distributive property for radicals.
Multiply all terms by 
Combine terms under radicals.
Look for perfect square factors under each radical. 


Since both radicals are the same, we can add them.
Compare your answer with the correct one above
Simplify the radical expression.
![\sqrt[3]{-64x^{6}y^{12}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/26625/gif.latex)
Simplify the radical expression.
![\sqrt[3]{-64x^{6}y^{12}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/26625/gif.latex)
Look for perfect cubes within each term. This will allow us to factor out of the radical.
![\sqrt[3]{-64}*\sqrt[3]{x^6}*\sqrt[3]{y^{12}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/85063/gif.latex)
![\sqrt[3]{-4*-4*-4}*\sqrt[3]{x^2*x^2*x^2}*\sqrt[3]{y^4*y^4*y^4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/119850/gif.latex)
Simplify.

Look for perfect cubes within each term. This will allow us to factor out of the radical.
Simplify.
Compare your answer with the correct one above
Which of the following expressions is equal to the following expression?

Which of the following expressions is equal to the following expression?

First, break down the component parts of the square root:

Combine like terms in a way that will let you pull some of them out from underneath the square root symbol:

Pull out the terms with even exponents and simplify:

First, break down the component parts of the square root:
Combine like terms in a way that will let you pull some of them out from underneath the square root symbol:
Pull out the terms with even exponents and simplify:
Compare your answer with the correct one above
Which of the following is equal to the following expression?

Which of the following is equal to the following expression?

First, break down the components of the square root:

Combine like terms. Remember, when multiplying exponents, add them together:

Factor out the common factor of  :
:


Factor the  :
:

Combine the factored  with the
with the  :
:

Now, you can pull  out from underneath the square root sign as
out from underneath the square root sign as  :
:

First, break down the components of the square root:
Combine like terms. Remember, when multiplying exponents, add them together:
Factor out the common factor of 
Factor the 
Combine the factored 

Now, you can pull 

Compare your answer with the correct one above
Which of the following expression is equal to

Which of the following expression is equal to

When simplifying a square root, consider the factors of each of its component parts:

Combine like terms:

Remove the common factor,  :
:

Pull the  outside of the equation as
outside of the equation as  :
:

When simplifying a square root, consider the factors of each of its component parts:
Combine like terms:
Remove the common factor, 
Pull the 

Compare your answer with the correct one above
Simplify: 
Simplify:
Rewrite  in their imaginary terms.
in their imaginary terms.


Rewrite 
Compare your answer with the correct one above
For  , what is the sum of
, what is the sum of  and its complex conjugate?
and its complex conjugate?
For 

The complex conjugate of a complex number  is
is  , so
, so  has
has  as its complex conjugate. The sum of the two numbers is
as its complex conjugate. The sum of the two numbers is




The complex conjugate of a complex number 



Compare your answer with the correct one above
Add  and its complex conjugate.
and its complex conjugate.
Add 
The complex conjugate of a complex number  is
is  . Therefore, the complex conjugate of
. Therefore, the complex conjugate of  is
is  ; add them by adding real parts and adding imaginary parts, as follows:
; add them by adding real parts and adding imaginary parts, as follows:


 ,
,
the correct response.
The complex conjugate of a complex number 




the correct response.
Compare your answer with the correct one above
Add  to its complex conjugate.
to its complex conjugate.
Add 
The complex conjugate of a complex number  is
is  . Therefore, the complex conjugate of
. Therefore, the complex conjugate of  is
is  ; add them by adding real parts and adding imaginary parts, as follows:
; add them by adding real parts and adding imaginary parts, as follows:




The complex conjugate of a complex number 



Compare your answer with the correct one above
An arithmetic sequence begins as follows:

Give the next term of the sequence
An arithmetic sequence begins as follows:
Give the next term of the sequence
The common difference  of an arithmetic sequence can be found by subtracting the first term from the second:
of an arithmetic sequence can be found by subtracting the first term from the second:


Add this to the second term to obtain the desired third term:
 .
.
The common difference 
Add this to the second term to obtain the desired third term:

Compare your answer with the correct one above
Evaluate:

Evaluate:
A power of  can be evaluated by dividing the exponent by 4 and noting the remainder. The power is determined according to the following table:
can be evaluated by dividing the exponent by 4 and noting the remainder. The power is determined according to the following table:

 , so
, so 
 , so
, so 
 , so
, so 
 , so
, so 
Substituting:




A power of 




Substituting:
Compare your answer with the correct one above
Evaluate:

Evaluate:
A power of  can be evaluated by dividing the exponent by 4 and noting the remainder. The power is determined according to the following table:
can be evaluated by dividing the exponent by 4 and noting the remainder. The power is determined according to the following table:

 , so
, so 
 , so
, so 
 , so
, so 
 , so
, so 
Substituting:



Collect real and imaginary terms:


A power of 




Substituting:
Collect real and imaginary terms:
Compare your answer with the correct one above
Simplify: 
Simplify:
It can be easier to line real and imaginary parts vertically to keep things organized, but in essence, combine like terms (where 'like' here means real or imaginary):



It can be easier to line real and imaginary parts vertically to keep things organized, but in essence, combine like terms (where 'like' here means real or imaginary):
Compare your answer with the correct one above
Let  . What is the following equivalent to, in terms of
. What is the following equivalent to, in terms of  :
:

Let 

Solve for x first in terms of y, and plug back into the equation.

Then go back to the equation you are solving for:
 substitute in
substitute in

Solve for x first in terms of y, and plug back into the equation.
Then go back to the equation you are solving for:

Compare your answer with the correct one above
For which of the following values of  is the value of
is the value of  least?
least?
For which of the following values of 

 is the same as
is the same as  , which means that the bigger the answer to
, which means that the bigger the answer to  is, the smaller the fraction will be.
is, the smaller the fraction will be.
Therefore,  is the correct answer because
is the correct answer because
 .
.



Therefore, 

Compare your answer with the correct one above