Solving Word Problems - SAT Math
Card 0 of 352
How many  are in
are in 
How many 
To solve this problem we can make proportions.
We know that  and we can use
and we can use  as our unknown.
as our unknown.

Next, we want to cross multiply and divide to isolate the on one side.


The  will cancel and we are left with
will cancel and we are left with 
To solve this problem we can make proportions.
We know that 

Next, we want to cross multiply and divide to isolate the on one side.
The 
Compare your answer with the correct one above
How many  are in
are in 
How many 
To solve this problem we can make proportions.
We know that  and we can use
and we can use 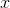 as our unknown.
as our unknown.

Next, we want to cross multiply and divide to isolate the on one side.


The  will cancel and we are left with
will cancel and we are left with 
To solve this problem we can make proportions.
We know that 
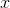
Next, we want to cross multiply and divide to isolate the on one side.
The 
Compare your answer with the correct one above
A carpenter is making a model house and he buys  of crown molding to use as accent pieces. He needs
of crown molding to use as accent pieces. He needs  of the molding for the house. How many feet of the material does he need to finish the model?
of the molding for the house. How many feet of the material does he need to finish the model?
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are  in
in  . We can write this relationship as the following ratio:
. We can write this relationship as the following ratio:

We know that the carpenter needs  of material to finish the house. We can write this as a ratio using the variable
of material to finish the house. We can write this as a ratio using the variable  to substitute the amount of feet.
to substitute the amount of feet.

Now, we can solve for  by creating a proportion using our two ratios.
by creating a proportion using our two ratios.

Cross multiply and solve for  .
.

Simplify.

Divide both sides by  .
.

Solve.

The carpenter needs  of material.
of material.
We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
The carpenter needs 
Compare your answer with the correct one above
A carpenter is making a model house and he buys  of crown moulding to use as accent pieces. He needs
of crown moulding to use as accent pieces. He needs  of the moulding for the house. How many feet of the material does he need to finish the model?
of the moulding for the house. How many feet of the material does he need to finish the model?
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are  in
in  . We can write this relationship as the following ratio:
. We can write this relationship as the following ratio:

We know that the carpenter needs  of material to finish the house. We can write this as a ratio using the variable
of material to finish the house. We can write this as a ratio using the variable  to substitute the amount of feet.
to substitute the amount of feet.

Now, we can solve for  by creating a proportion using our two ratios.
by creating a proportion using our two ratios.

Cross multiply and solve for  .
.

Simplify.

Divide both sides by  .
.

Solve.

Reduce.

The carpenter needs  of material.
of material.
We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Compare your answer with the correct one above
A carpenter is making a model house and he buys  of crown moulding to use as accent pieces. He needs
of crown moulding to use as accent pieces. He needs  of the moulding for the house. How many feet of the material does he need to finish the model?
of the moulding for the house. How many feet of the material does he need to finish the model?
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are  in
in  . We can write this relationship as the following ratio:
. We can write this relationship as the following ratio:

We know that the carpenter needs  of material to finish the house. We can write this as a ratio using the variable
of material to finish the house. We can write this as a ratio using the variable  to substitute the amount of feet.
to substitute the amount of feet.

Now, we can solve for  by creating a proportion using our two ratios.
by creating a proportion using our two ratios.

Cross multiply and solve for  .
.

Simplify.

Divide both sides by  .
.

Solve.

The carpenter needs  of material.
of material.
We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
The carpenter needs 
Compare your answer with the correct one above
A carpenter is making a model house and he buys  of crown moulding to use as accent pieces. He needs
of crown moulding to use as accent pieces. He needs  of the moulding for the house. How many feet of the material does he need to finish the model?
of the moulding for the house. How many feet of the material does he need to finish the model?
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are  in
in  . We can write this relationship as the following ratio:
. We can write this relationship as the following ratio:

We know that the carpenter needs  of material to finish the house. We can write this as a ratio using the variable
of material to finish the house. We can write this as a ratio using the variable  to substitute the amount of feet.
to substitute the amount of feet.

Now, we can solve for  by creating a proportion using our two ratios.
by creating a proportion using our two ratios.

Cross multiply and solve for  .
.

Simplify.

Divide both sides by  .
.

Solve.

Reduce.

The carpenter needs  of material.
of material.
We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Compare your answer with the correct one above
A carpenter is making a model house and he buys  of crown moulding to use as accent pieces. He needs
of crown moulding to use as accent pieces. He needs  of the moulding for the house. How many feet of the material does he need to finish the model?
of the moulding for the house. How many feet of the material does he need to finish the model?
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are  in
in  . We can write this relationship as the following ratio:
. We can write this relationship as the following ratio:

We know that the carpenter needs  of material to finish the house. We can write this as a ratio using the variable
of material to finish the house. We can write this as a ratio using the variable  to substitute the amount of feet.
to substitute the amount of feet.

Now, we can solve for  by creating a proportion using our two ratios.
by creating a proportion using our two ratios.

Cross multiply and solve for  .
.

Simplify.

Divide both sides by  .
.

Solve.

Reduce.

The carpenter needs  of material.
of material.
We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Compare your answer with the correct one above
A carpenter is making a model house and he buys  of crown moulding to use as accent pieces. He needs
of crown moulding to use as accent pieces. He needs  of the moulding for the house. How many feet of the material does he need to finish the model?
of the moulding for the house. How many feet of the material does he need to finish the model?
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are  in
in  . We can write this relationship as the following ratio:
. We can write this relationship as the following ratio:

We know that the carpenter needs  of material to finish the house. We can write this as a ratio using the variable
of material to finish the house. We can write this as a ratio using the variable  to substitute the amount of feet.
to substitute the amount of feet.

Now, we can solve for  by creating a proportion using our two ratios.
by creating a proportion using our two ratios.

Cross multiply and solve for  .
.

Simplify.

Divide both sides by  .
.

Solve.

The carpenter needs  of material.
of material.
We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
The carpenter needs 
Compare your answer with the correct one above
A carpenter is making a model house and he buys  of crown moulding to use as accent pieces. He needs
of crown moulding to use as accent pieces. He needs  of the moulding for the house. How many feet of the material does he need to finish the model?
of the moulding for the house. How many feet of the material does he need to finish the model?
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are  in
in  . We can write this relationship as the following ratio:
. We can write this relationship as the following ratio:

We know that the carpenter needs  of material to finish the house. We can write this as a ratio using the variable
of material to finish the house. We can write this as a ratio using the variable  to substitute the amount of feet.
to substitute the amount of feet.

Now, we can solve for  by creating a proportion using our two ratios.
by creating a proportion using our two ratios.

Cross multiply and solve for  .
.

Simplify.

Divide both sides by  .
.

Solve.

Reduce.

The carpenter needs  of material.
of material.
We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Compare your answer with the correct one above
A carpenter is making a model house and he buys  of crown moulding to use as accent pieces. He needs
of crown moulding to use as accent pieces. He needs  of the moulding for the house. How many feet of the material does he need to finish the model?
of the moulding for the house. How many feet of the material does he need to finish the model?
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are  in
in  . We can write this relationship as the following ratio:
. We can write this relationship as the following ratio:

We know that the carpenter needs  of material to finish the house. We can write this as a ratio using the variable
of material to finish the house. We can write this as a ratio using the variable  to substitute the amount of feet.
to substitute the amount of feet.

Now, we can solve for  by creating a proportion using our two ratios.
by creating a proportion using our two ratios.

Cross multiply and solve for  .
.

Simplify.

Divide both sides by  .
.

Solve.

Reduce.

The carpenter needs  of material.
of material.
We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Compare your answer with the correct one above
A carpenter is making a model house and he buys  of crown moulding to use as accent pieces. He needs
of crown moulding to use as accent pieces. He needs  of the moulding for the house. How many feet of the material does he need to finish the model?
of the moulding for the house. How many feet of the material does he need to finish the model?
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are  in
in  . We can write this relationship as the following ratio:
. We can write this relationship as the following ratio:

We know that the carpenter needs  of material to finish the house. We can write this as a ratio using the variable
of material to finish the house. We can write this as a ratio using the variable  to substitute the amount of feet.
to substitute the amount of feet.

Now, we can solve for  by creating a proportion using our two ratios.
by creating a proportion using our two ratios.

Cross multiply and solve for  .
.

Simplify.

Divide both sides by  .
.

Solve.

Reduce.

The carpenter needs  of material.
of material.
We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Compare your answer with the correct one above
A carpenter is making a model house and he buys  of crown moulding to use as accent pieces. He needs
of crown moulding to use as accent pieces. He needs  of the moulding for the house. How many feet of the material does he need to finish the model?
of the moulding for the house. How many feet of the material does he need to finish the model?
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are  in
in  . We can write this relationship as the following ratio:
. We can write this relationship as the following ratio:

We know that the carpenter needs  of material to finish the house. We can write this as a ratio using the variable
of material to finish the house. We can write this as a ratio using the variable  to substitute the amount of feet.
to substitute the amount of feet.

Now, we can solve for  by creating a proportion using our two ratios.
by creating a proportion using our two ratios.

Cross multiply and solve for  .
.

Simplify.

Divide both sides by  .
.

Solve.

Reduce.

The carpenter needs  of material.
of material.
We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Compare your answer with the correct one above
A carpenter is making a model house and he buys  of crown moulding to use as accent pieces. He needs
of crown moulding to use as accent pieces. He needs  of the moulding for the house. How many additional feet of the material will he need to purchase to finish the model?
of the moulding for the house. How many additional feet of the material will he need to purchase to finish the model?
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are  in
in  . We can write this relationship as the following ratio:
. We can write this relationship as the following ratio:

We know that the carpenter needs  of material to finish the house. We can write this as a ratio using the variable
of material to finish the house. We can write this as a ratio using the variable  to substitute the amount of feet.
to substitute the amount of feet.

Now, we can solve for  by creating a proportion using our two ratios.
by creating a proportion using our two ratios.

Cross multiply and solve for  .
.

Simplify.

Divide both sides by  .
.

Solve.

The carpenter needs  of material. Since he already has
of material. Since he already has  he will need to purchase
he will need to purchase  more to finish the project.
more to finish the project.
We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
The carpenter needs 


Compare your answer with the correct one above
A carpenter is making a model house and he buys  of crown moulding to use as accent pieces. He needs
of crown moulding to use as accent pieces. He needs  of the moulding for the house. How many feet of the material does he need to finish the model?
of the moulding for the house. How many feet of the material does he need to finish the model?
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are  in
in  . We can write this relationship as the following ratio:
. We can write this relationship as the following ratio:

We know that the carpenter needs  of material to finish the house. We can write this as a ratio using the variable
of material to finish the house. We can write this as a ratio using the variable  to substitute the amount of feet.
to substitute the amount of feet.

Now, we can solve for  by creating a proportion using our two ratios.
by creating a proportion using our two ratios.

Cross multiply and solve for  .
.

Simplify.

Divide both sides by  .
.

Solve.

Reduce.

The carpenter needs  of material.
of material.
We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Compare your answer with the correct one above
Erin is making thirty shirts for her upcoming family reunion. At the reunion she is selling each shirt for \$18 apiece. If each shirt cost her \$10 apiece to make, how much profit does she make if she only sells 25 shirts at the reunion?
Erin is making thirty shirts for her upcoming family reunion. At the reunion she is selling each shirt for \$18 apiece. If each shirt cost her \$10 apiece to make, how much profit does she make if she only sells 25 shirts at the reunion?
This problem involves two seperate multiplication problems. Erin will make \$450 at the reunion but supplies cost her \$300 to make the shirts. So her profit is \$150.
This problem involves two seperate multiplication problems. Erin will make \$450 at the reunion but supplies cost her \$300 to make the shirts. So her profit is \$150.
Compare your answer with the correct one above
Write as an equation:
"Ten added to the product of a number and three is equal to twice the number."
Write as an equation:
"Ten added to the product of a number and three is equal to twice the number."
Let  represent the unknown quantity.
represent the unknown quantity.
The first expression:
"The product of a number and three" is three times this number, or

"Ten added to the product" is

The second expression:
"Twice the number" is two times the number, or
 .
.
The desired equation is therefore
 .
.
Let 
The first expression:
"The product of a number and three" is three times this number, or
"Ten added to the product" is
The second expression:
"Twice the number" is two times the number, or

The desired equation is therefore

Compare your answer with the correct one above
Write as an equation:
Five-sevenths of the difference of a number and nine is equal to forty.
Write as an equation:
Five-sevenths of the difference of a number and nine is equal to forty.
"The difference of a number and nine" is the result of a subtraction of the two, so we write this as

"Five-sevenths of" this difference is the product of  and this, or
and this, or

This is equal to forty, so write the equation as

"The difference of a number and nine" is the result of a subtraction of the two, so we write this as
"Five-sevenths of" this difference is the product of 
This is equal to forty, so write the equation as
Compare your answer with the correct one above
Write as an equation:
Twice the sum of a number and ten is equal to the difference of the number and one half.
Write as an equation:
Twice the sum of a number and ten is equal to the difference of the number and one half.
Let  represent the unknown number.
represent the unknown number.
"The sum of a number and ten" is the expression  . "Twice" this sum is two times this expression, or
. "Twice" this sum is two times this expression, or
 .
.
"The difference of the number and one half" is a subtraction of the two, or

Set these equal, and the desired equation is

Let 
"The sum of a number and ten" is the expression 

"The difference of the number and one half" is a subtraction of the two, or
Set these equal, and the desired equation is
Compare your answer with the correct one above
If a rectangle possesses a width of  and has a perimeter of
and has a perimeter of  , then what is the length?
, then what is the length?
If a rectangle possesses a width of 

In order to solve this problem, we need to recall the formula for perimeter of a rectangle:

We can substitute in our known values and solve for our unknown variable (i.e. length):


We want to isolate the  to one side of the equation. In order to do this, we will first subtract
to one side of the equation. In order to do this, we will first subtract  from both sides of the equation.
from both sides of the equation.
![\frac{\begin{array}[b]{r}36=2l+16\ -16\ \ \ \ \ \ -16\end{array}}{\\20=2l}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/924152/gif.latex)
Next, we can divide each side by 
![\frac{\begin{array}[b]{r}\frac{20}{2}=\frac{2l}{2}\\end{array}}{10=l}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/924154/gif.latex)
The length of the rectangle is 
In order to solve this problem, we need to recall the formula for perimeter of a rectangle:
We can substitute in our known values and solve for our unknown variable (i.e. length):
We want to isolate the 

Next, we can divide each side by
The length of the rectangle is
Compare your answer with the correct one above
If a rectangle possesses a width of  and has a perimeter of
and has a perimeter of  , then what is the length?
, then what is the length?
If a rectangle possesses a width of 

In order to solve this problem, we need to recall the formula for perimeter of a rectangle:

We can substitute in our known values and solve for our unknown variable (i.e. length):


We want to isolate the  to one side of the equation. In order to do this, we will first subtract
to one side of the equation. In order to do this, we will first subtract  from both sides of the equation.
from both sides of the equation.
![\frac{\begin{array}[b]{r}36=2l+24\ -24\ \ \ \ \ \ -24\end{array}}{\\12=2l}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/924287/gif.latex)
Next, we can divide each side by 
![\frac{\begin{array}[b]{r}\frac{12}{2}=\frac{2l}{2}\\end{array}}{6=l}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/924288/gif.latex)
The length of the rectangle is 
In order to solve this problem, we need to recall the formula for perimeter of a rectangle:
We can substitute in our known values and solve for our unknown variable (i.e. length):
We want to isolate the 

Next, we can divide each side by
The length of the rectangle is
Compare your answer with the correct one above