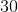SSAT Upper Level Quantitative - Geometry

What is the slope of the line that passes through the points $(-1,4) \text{ and } (-5,1)$ ?

$\frac{3}{4}$

$-\frac{3}{4}$

$\frac{4}{3}$

$-\frac{4}{3}$

Explanation

Use the following formula to find the slope:

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

Substituting the values from the points given, we get the following slope:

$\text{Slope}=\frac{1-4}{-5-(-1)}=\frac{-3}{-4}=\frac{3}{4}$

Which of the following lines is parallel to the line ?

$y=\frac{1}{4}x-2$

$y=-\frac{1}{4}x+2$

Explanation

For two lines to be parallel, their slopes must be the same. Thus, the line that is parallel to the given one must also have a slope of .

Find the area of a regular hexagon that has side lengths of .

$54\sqrt3$

$36\sqrt3$

$48\sqrt3$

Explanation

Use the following formula to find the area of a regular hexagon:

$\text{Area}=\frac{3\sqrt3}{2}\times \text{side}^2$ .

Now, substitute in the length of the side into this equation.

$\text{Area}=\frac{3\sqrt3}{2}\times6^2$

$\text{Area}=\frac{3\sqrt3}{2}\times 36$

$\text{Area}=\frac{108\sqrt3}{2}=54\sqrt3$

The area of a rectangle is square feet. The width of the rectangle is four-sevenths of its length. Give the length of the rectangle in inches in terms of .

$6\sqrt{ 7K }$

$\frac{ \sqrt{ 7K } }{24}$

$\frac{ \sqrt{ 7K } }{2}$

$\frac{7K} {48}$

Explanation

Let be the length in feet. Then the width of the rectangle in feet is four-sevenths of this, or $\frac{4}{7}L$ . The area is equal to the product of the length and the width, so set up this equation and solve for :

$\frac{4}{7}L \cdot L = K$

$\frac{4}{7}L ^{2}= K$

$\frac{7} {4}\cdot \frac{4}{7}L ^{2}= \frac{7} {4}\cdot K$

$L ^{2}= \frac{7K} {4}$

$L =\sqrt{ \frac{7K} {4}} =\frac{ \sqrt{ 7K } }{\sqrt{4}}=\frac{ \sqrt{ 7K } }{2}$

Since this is the length in feet, we multiply this by 12 to get the length in inches:

$\frac{ \sqrt{ 7K } }{2} \cdot 12 = 6\sqrt{ 7K }$

Find the area of a regular pentagon that has a side length of and an apothem of .

Explanation

To find the area of a regular polygon,

$\text{Area}=\frac{1}{2}(Perimeter)(apothem)$

To find the perimeter of the pentagon,

$\text{Perimeter}=5(side)$

For the given pentagon,

$\text{Perimeter}=5\times6=30$

So then, to find the area of the pentagon,

$\text{Area}=\frac{1}{2}(30)(2)=30$

Find the angle value of .

$46^{\circ}$

$56^{\circ}$

$36^{\circ}$

$66^{\circ}$

Explanation

All the angles in a triangle add up to degrees.

$90^{\circ}+44^{\circ}+y=180^{\circ}$

$134^{\circ}+y=180^{\circ}$

$134^{\circ}+y-134^{\circ}=180^{\circ}-134^{\circ}$

$y=46^{\circ}$

Which of the following lines is parallel with the line $y=-\frac{1}{5}x+1$ ?

$y=-\frac{1}{5}x+9$

$y=\frac{1}{5}x-2$

Explanation

Parallel lines have the same slope. The slope of a line in slope-intercept form is the value of . So, the slope of the line $y=-\frac{1}{5}x+1$ is $-\frac{1}{5}$ . That means that for the two lines to be parallel, the slope of the second line must also be $-\frac{1}{5}$ .