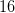ACT Math : ACT Math
Study concepts, example questions & explanations for ACT Math
All ACT Math Resources
Example Questions
Example Question #1 : How To Divide Negative Numbers
Solve for 
Begin by isolating your variable.
Subtract 
Next, subtract 
Then, divide both sides by 
Recall that division of a negative by a negative gives you a positive, therefore:
Example Question #1 : How To Divide Negative Numbers
Solve the following equation:
The rule for dividing negative numbers is the same as for multiplying negative numbers.
If both numbers are negative, you will get a positive answer.
If either number is positive, and the other is negative, you will get a negative answer.
Therefore:
Example Question #1 : How To Divide Negative Numbers
Choose the answer which best solves the following equation:
To solve, first put the equation in terms of 
First multiply the x to both sides.
Now divide by 12 to solve for x.
Here, because one of the numbers in the equation is positive, and the other is negative, the answer must be a negative number:
Example Question #1621 : Act Math
Add:
Simply the signs before solving. A positive sign multiplied with a negative sign will convert the sign to a negative, and a negative multiplied with a negative will convert the sign to a positive.
Example Question #1622 : Act Math
Solve:
Starting at 
Example Question #1 : How To Add Negative Numbers
Solve:
Adding 
Example Question #1623 : Act Math
Add
Starting at 
Example Question #1 : Number Line
How many integers are there between 
Since we are not including 
If negative numbers are difficult for you to understand you can think of it this way. Since both values are negative and we are looking for the amount of integers between them we can solve the problem by subtracting 2 from 17 and then another one since we don't want to include the endpoints.
Example Question #1 : Graphing An Inequality With A Number Line
On a real number line, x1 = -4 and x2 = 14. What is the distance between these two points?
18
-18
4
10
18
The distance between two points is always positive. We calculate lx2 - x1l, which will give us the distance between the points.
|14- (-4)| = |14+4| = |18| = 18
Example Question #2 : Graphing An Inequality With A Number Line
Which of the following is a graph for the values of 
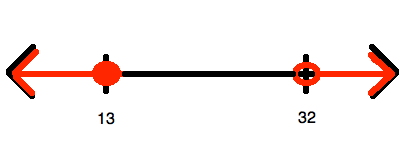
To begin, you must simplify so that you "isolate" 
Now, this inequality represents all of the numbers between 13 and 32. However, it does include 
All ACT Math Resources
