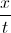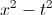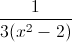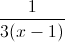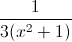Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : ACT Math

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Expressions

2x-12=24

3y-15=60

Find the product of and .

Possible Answers:

450

260

325

120

144

Correct answer:

450

Explanation:

Solve the first equation for .

2x-12=24

2x=36

x=18

Solve the second equation for .

3y-15=60

3y=75

y=25

The final step is to multiply and .

xy = (18)(25)=450

Report an Error

Example Question #1 : Expressions

The following table shows the temperature of a cup of coffee at different times

Time 1:09 1:11 1:13 1:15 1:17

Temperature (ºF) 187.1 184.4 181.7 179.0 176.3

If this trend continues, what will the temperature of the coffee at minute 1:25?

Possible Answers:

168.3°F

171.0°F

165.5°F

160.2°F

162.9°F

Correct answer:

165.5°F

Explanation:

The table shows that for every two minutes, the temperature of the coffee lowers 2.7ºF. At 1:25, 16 minutes, or eight 2-minute intervals have passed, and the temperature of the coffee has lowered by 8*2.7ºF, reaching a temperature of 165.5ºF.

Report an Error

Example Question #2 : Rational Expressions

Amy buys concert tickets for herself and her friends. She initially buys them at $40/ticket. Weeks later, her other friends ask her to buy them tickets, but the prices have increased to $54. Amy buys 7 tickets total and spends $350. How many tickets has she paid $40 on?

Possible Answers:

Correct answer:

Explanation:

Amy has bought 7 tickets, x of them at $40/ticket, and the remaining 7-x at $54/ticket. She spends at total of

$\\ \\ \$350 = 40x + (54)(7-x) = 40x + 378 – 54x = 378 – 14x\rightarrow \\ 14x = 378-350 = 28 \rightarrow x =2.$

Report an Error

Example Question #1 : Expressions

What is

$\frac{3}{\sqrt{6}}$ ?

Possible Answers:

$\frac{\sqrt{6}}{3}$

$\frac{\sqrt{12}}{3}$

$\frac{\sqrt{3}}{3}$

$\frac{\sqrt{3}}{2}$

$\frac{\sqrt{6}}{2}$

Correct answer:

$\frac{\sqrt{6}}{2}$

Explanation:

To find an equivalency we must rationalize the denominator.

To rationalize the denominator multiply the numerator and denominator by the denominator.

$\frac{3}{\sqrt{6}}$ $*\frac{\sqrt{6}}{\sqrt{6}}=$

$\frac{3*\sqrt{6}}{6}=$

To simplify completely, factor out a three from the numerator and denominator resulting in the final solution.

$\frac{\sqrt{6}}{2}$

Report an Error

Example Question #2401 : Act Math

Simplify:

$\frac{4}{x-3}-\frac{12}{x+1}$

Possible Answers:

$\frac{-8}{x^2-2}$

$\frac{-8}{x-2}$

$\frac{40-8x}{x^2-2x-3}$

$\frac{4x-3}{x^2-x+3}$

$\frac{4}{x-1}$

Correct answer:

$\frac{40-8x}{x^2-2x-3}$

Explanation:

The common denominator of these two fractions simply is the product of the two denominators, namely:

(x-3)(x+1)

Thus, you will need to multiply each fraction's numerator and denominator by the opposite fraction's denominator:

$\frac{4}{x-3}-\frac{12}{x+1}=\frac{4}{x-3}*\frac{x+1}{x+1}-\frac{12}{x+1}*\frac{x-3}{x-3}$

Let's first simplify the numerator:

$\frac{4(x+1)-12(x-3)}{(x-3)(x+1)}$

$\frac{4x+4-12x+36}{(x-3)(x+1)}$

$\frac{-8x+40}{(x-3)(x+1)}$ , which is the simplest form you will need for this question.

However, the correct answer has the denominator multiplied out. Merely FOIL (x-3)(x+1) :

$\frac{40-8x}{x^2-2x-3}$

Report an Error

Example Question #1 : How To Subtract Rational Expressions With Different Denominators

Simplify:

$\frac{4x}{(x+4)}-\frac{2}{x^2+6x+8}$

Possible Answers:

$\frac{x}{x^2+5x+4}$

$\frac{4x^2+6x-1}{x^2+6x+8}$

$\frac{2x-1}{x^2+5x+4}$

$\frac{4x^2+6x-8}{x^2+6x+8}$

$\frac{4x^2+8x-2}{x^2+6x+8}$

Correct answer:

$\frac{4x^2+8x-2}{x^2+6x+8}$

Explanation:

Always start the simplification of rational expressions with quadratic denominators by factoring the denominator that has a squared element:

$\frac{4x}{(x+4)}-\frac{2}{x^2+6x+8} = \frac{4x}{(x+4)}-\frac{2}{(x+4)(x+2)}$

Thus, we need to multiply the numerator and denominator of the first term by (x+2) :

$\frac{4x}{(x+4)}*\frac{x+2}{x+2}-\frac{2}{(x+4)(x+2)}$

Distribute:

$\frac{4x^2+8x}{(x+4)(x+2)}-\frac{2}{(x+4)(x+2)}$

This is simply:

$\frac{4x^2+8x-2}{(x+4)(x+2)}$

You cannot factor the top in any way that would help you to cancel anything. Therefore, the answer stands as it does. You need to FOIL the denominator back out, as your correct answer is in that form:

$\frac{4x^2+8x-2}{x^2+6x+8}$

Report an Error

Example Question #911 : Algebra

Simplify:

$\frac{4x}{x^2-x-6}-\frac{2x-4}{x^2-9}$

Possible Answers:

$\frac{2x+4}{x^2-x-6}$

$\frac{2x^2+12x+8}{(x-3)(x+3)(x+2)}$

$\frac{x^2+5x+1}{(x-3)(x+3)}$

$\frac{x^2+6x+2}{(x-3)(x+2)}$

$\frac{2x+4}{3-x}$

Correct answer:

$\frac{2x^2+12x+8}{(x-3)(x+3)(x+2)}$

Explanation:

Begin by factoring your denominators:

$\frac{4x}{x^2-x-6}-\frac{2x-4}{x^2-9}=\frac{4x}{(x-3)(x+2)}-\frac{2x-4}{(x+3)(x-3)}$

Therefore, the common denominator of our fractions is:

(x-3)(x+3)(x+2)

This will require you to multiply the first fraction by $\frac{x+3}{x+3}$ and the second by $\frac{x+2}{x+2}$ . This gives you:

$\frac{4x(x+3)-(2x-4)(x+2)}{(x-3)(x+3)(x+2)}$

Now, FOIL the second member and distribute the first:

$\frac{4x^2+12x-(2x^2-8)}{(x-3)(x+3)(x+2)}$

Next, distribute the subtraction:

$\frac{4x^2+12x-2x^2+8}{(x-3)(x+3)(x+2)}$

Finally, simplify:

$\frac{2x^2+12x+8}{(x-3)(x+3)(x+2)}$

Report an Error

Example Question #1 : How To Divide Rational Expressions

What is $\frac{x^{2} + 11x + 28}{x+7}$ ?

Possible Answers:

x -4

x +4

$x^{2} +4$

x+7

x + 11

Correct answer:

x +4

Explanation:

$x^{2} + 11x + 28$ factors to (x + 4)(x+7) . Thus, $\frac{(x+4)(x+7)}{x+7}$ . Canceling out like terms leads to x+4 .

Report an Error

Example Question #2 : Rational Expressions

Which of the following is equivalent to $\dpi{100} \frac{(\frac{1}{t}-\frac{1}{x})}{x-t}$ ? Assume that denominators are always nonzero.

Possible Answers:

$x-t$

$(xt)^{-1}$

$\frac{x}{t}$

$t-x$

$x^{2}-t^{2}$

Correct answer:

$(xt)^{-1}$

Explanation:

We will need to simplify the expression $\frac{(\frac{1}{t}-\frac{1}{x})}{x-t}$ . We can think of this as a large fraction with a numerator of $\frac{1}{t}-\frac{1}{x}$ and a denominator of $\dpi{100} x-t$ .

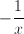
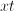
In order to simplify the numerator, we will need to combine the two fractions. When adding or subtracting fractions, we must have a common denominator. $\frac{1}{t}$ has a denominator of $\dpi{100} t$ , and $\dpi{100} -\frac{1}{x}$ has a denominator of $\dpi{100} x$ . The least common denominator that these two fractions have in common is $\dpi{100} xt$ . Thus, we are going to write equivalent fractions with denominators of $\dpi{100} xt$ .

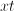
In order to convert the fraction $\dpi{100} \frac{1}{t}$ to a denominator with $\dpi{100} xt$ , we will need to multiply the top and bottom by $\dpi{100} x$ .

$\frac{1}{t}=\frac{1\cdot x}{t\cdot x}=\frac{x}{xt}$

Similarly, we will multiply the top and bottom of $\dpi{100} -\frac{1}{x}$ by $\dpi{100} t$ .

$\frac{1}{x}=\frac{1\cdot t}{x\cdot t}=\frac{t}{xt}$

We can now rewrite $\frac{1}{t}-\frac{1}{x}$ as follows:

$\frac{1}{t}-\frac{1}{x}$ = $\frac{x}{xt}-\frac{t}{xt}=\frac{x-t}{xt}$

Let's go back to the original fraction $\frac{(\frac{1}{t}-\frac{1}{x})}{x-t}$ . We will now rewrite the numerator:

$\frac{(\frac{1}{t}-\frac{1}{x})}{x-t}$ = $\frac{\frac{x-t}{xt}}{x-t}$

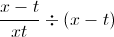
To simplify this further, we can think of $\frac{\frac{x-t}{xt}}{x-t}$ as the same as $\frac{x-t}{xt}\div (x-t)$ . When we divide a fraction by another quantity, this is the same as multiplying the fraction by the reciprocal of that quantity. In other words, $a\div b=a\cdot \frac{1}{b}$ .

$\frac{x-t}{xt}\div (x-t)$ = $\frac{x-t}{xt}\cdot \frac{1}{x-t}$ $=\frac{x-t}{xt(x-t)}$ $= \frac{1}{xt}$

Lastly, we will use the property of exponents which states that, in general, $\frac{1}{a}=a^{-1}$ .

$\frac{1}{xt}=(xt)^{-1}$

The answer is $(xt)^{-1}$ .

Report an Error

Example Question #1 : Rational Expressions

Simplify:

$\frac{x^{2}+x-2}{3x^{2} + 9x + 6} \div (x-1)$

Possible Answers:

$\frac{1}{3(x^{2}-2)}$

$\frac{1}{3(x+2)}$

$\frac{1}{3(x-1)}$

$\frac{1}{3(x^{2}+1)}$

$\frac{1}{3(x+1)}$

Correct answer:

$\frac{1}{3(x+1)}$

Explanation:

Multiply by the reciprocal of $\frac{x-1}1{}$ .

$\frac{x^{2}+x-2}{3x^{2}+9x+6} \cdot \frac{1}{x-1}$

Factor $\frac{(x-1)(x+2)}{3(x+2)(x+1)} \cdot \frac{1}{x-1}$

Divide by common factors.

$= \frac{1}{3(x+1)}$

Report an Error

View ACT Math Tutors

Chernyeh
Certified Tutor

Purdue University-Main Campus, Bachelor of Science, Business Administration and Management.

View ACT Math Tutors

Martine
Certified Tutor

University of South Florida-Main Campus, Bachelors, Science. Windsor University School of Medicine, Doctor of Medicine, Scien...

View ACT Math Tutors

Shimelis
Certified Tutor

Alemaya Uniersity of Agriculture, Bachelor, Agricultural Engineering. Alemaya University, Master's/Graduate, Agricultural Eng...

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

SAT Courses & Classes in Washington DC, ISEE Courses & Classes in Seattle, GRE Courses & Classes in Houston, Spanish Courses & Classes in Phoenix, ACT Courses & Classes in Washington DC, ISEE Courses & Classes in Atlanta, Spanish Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Philadelphia, SSAT Courses & Classes in Houston, SSAT Courses & Classes in Washington DC

Popular Test Prep

GMAT Test Prep in Chicago, SAT Test Prep in Atlanta, SSAT Test Prep in Los Angeles, ISEE Test Prep in Denver, ACT Test Prep in Phoenix, ACT Test Prep in Washington DC, GMAT Test Prep in New York City, GMAT Test Prep in Boston, GRE Test Prep in Los Angeles, LSAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : ACT Math

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #1 : Expressions

Example Question #1 : Expressions

Example Question #2 : Rational Expressions

Example Question #1 : Expressions

Example Question #2401 : Act Math

Example Question #1 : How To Subtract Rational Expressions With Different Denominators

Example Question #911 : Algebra

Example Question #1 : How To Divide Rational Expressions

Example Question #2 : Rational Expressions

Example Question #1 : Rational Expressions

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: