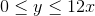The basic formula for a circle in the coordinate plane is , where  is the center of the circle with radius .

Since  refers to the y-coordinate of the center, and we know that any point on the x-axis has a y-coordinate of , we merely need to look for the equation in which k does not exist.

Note that despite meeting this requirement,  still does not qualify, as it is not an equation for a circle at all. Without including a value for , this equation describes a parabola.

The basic formula for a circle in the coordinate plane is , where  is the center of the circle with radius .

We know that , since that is the only way a diameter can pass through the circle and intercept an x-coordinate of  at both ends. , on the other hand, may be seen as halfway between one y-coordinate and the other y-coordinate. Averaging the two, we get:

, so  becomes our . Since the diameter is  units long, we know the radius is half that, so .

Thus, we have .

The formula for a circle is 

 is the coordinate of the center of the circle, therefore  and .

The area of a circle:  

Therefore:

Recall that the general form of the equation of a circle centered at the origin is:

x² + y² = r²

We know that the radius of our circle is five. Therefore, we know that the equation for our circle is:

x² + y² = 5²

x² + y² = 25

Now, the question asks for the positive y-coordinate when x = 2.  To solve this, simply plug in for x:

2² + y² = 25

4 + y² = 25

y² = 21

y = ±√(21)

Since our answer will be positive, it must be √(21).

The equation for a circle is (x - h)² + (y - k)² = r², where (h,k) is the center of the circle and r is the radius.

We can eliminate (x+3) +(y+2) = 4 and (x+3)² + (y+2)² = 64. The first equation does not square the terms in parentheses, and the second refers to a center of (-3,-2) rather than (3,2).

Drawing the line y = -2 and a point at (3,2) for the center of the circle, we see that the only way the line could be tangent to the circle is if it touches the bottom-most part of the circle, directly under the center. The point of intersection will be (3,-2). From this, we can see that the distance from the center to this point of intersection is 4 units between (3,2) and (3,-2). This means the radius of the circle is 4.

Use the center point and the radius in the formula for a circle to find the final answer: (x - 3)² + (y - 2)² = 16

To solve the inequality, the first step is to add  to both sides:

The second step is to divide both sides by :

To graph the inequality, you draw a straight number line. Fill in the numbers from  to infinity. Infinity can be designated by a ray. Be sure to fill in the number , since the equation indicated greater than OR equal to.

The graph should look like:

If we plug the points  and  into each equation, we find that these points work only in the equation . This circle has a radius of  and is centered at .

The key here is to look for the line whose slope is the negative reciprocal of the original slope.

In this case,  is the negative reciprocal of .

Therefore, the equation of the line which is perpendicular to the original equation is:

The inverse of a function has all the same points as the original function, except the x values and y values are reversed. The same rule applies to polygons such as triangles.