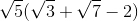Using PEMDAS helps us solve our equation step-by-step:

\(\displaystyle 2-5(7-3^2)^3 \div 2\) State the equation.

\(\displaystyle 2-5(7-9)^3 \div 2\) Solve inside the parenthesis first.

\(\displaystyle 2-5(-2)^3 \div 2\) Simplify inside the parenthesis.

\(\displaystyle 2-5(-8) \div 2\) Solve the exponent.

\(\displaystyle 2+ 40 \div 2\) Multiply.

\(\displaystyle 2+ 20\) Divide.

\(\displaystyle 22\) Add.

Thus, our answer is \(\displaystyle 22\).

We know that the first half of this equation is three less than half of a number. So, we look for those equations which divide a variable by two, showing \(\displaystyle \frac{x}{2}\). Next, we know to subtract \(\displaystyle 3\), so \(\displaystyle \frac{x}{2} -3\) must be the first half. Lastly, we know that this amount is more than the other half of our equation, so we eliminate the answers with \(\displaystyle < \).

"Which equation represents a quantity which, when squared, equals twice its own square root?" To answer, square a variable on one side of an equation.

\(\displaystyle x^ 2 =\)

Now, square root the variable on the other side.

\(\displaystyle x^2 = \sqrt{x}\)

Lastly, multiply the square root by \(\displaystyle 2\):

\(\displaystyle x^2 = 2\sqrt{x}\)

To solve, simply use PEMDAS to do the correct order of operations.

PEMDAS stands for,

Parentheses, Exponents, Multiplication/Division, Addition/Subtraction.

Thus,

\(\displaystyle 6+7*2-5+3*2\rightarrow 6+14-5+6=20+1=21\)

This problem requires proper order of operations. Remember the acronym for the order of operations: PEMDAS. This acronym will help you to remember the proper order for solving problems:

1. Parentheses
2. Exponents
3. Multiplication and Division (whichever comes first as you read the problem from left to right)
4. Addition and Subtraction (whichever comes first as you read the problem from left to right)

Let's start with the first expression:

\(\displaystyle 2x^2 - 2y\)

Substitute in our values for the x- and y-variables.

\(\displaystyle 2(4^2) - 2\times3\)

Step 1: Since there are no parentheses we will start with exponents.

\(\displaystyle 2(16) - 2\times3\)

Step 2: Multiplication

\(\displaystyle 2\times16 - 2\times3\)

\(\displaystyle 32 - 6\)

Step 3: Subtraction

\(\displaystyle 32-6=26\)

For the second expression, we will proceed in a similar fashion. Let's start with the first expression:

\(\displaystyle 2x^2-2y^2\)

Substitute in our values for the x- and y-variables.

\(\displaystyle 2(4^2)-2(3^2)\)

Step 1: Since there are no parentheses we will start with exponents.

\(\displaystyle 2(16)-2(9)\)

Step 2: Multiplication

\(\displaystyle 2\times 16-2\times9\)

\(\displaystyle 32-18\)

Step 3: Subtraction

\(\displaystyle 32-18=14\)

Last, the difference between the first expression and the second is as follows:

\(\displaystyle 26 -14 = 12\)

The correct choice is \(\displaystyle 12\)

To solve the equation \(\displaystyle \sqrt{2016} + \sqrt{896} = ?\), we can first factor the numbers under the square roots.

\(\displaystyle \sqrt{2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 3\cdot 3\cdot 7} + \sqrt{2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 7} = ?\)

When a factor appears twice, we can take it out of the square root.

\(\displaystyle 2\cdot 2\cdot 3\sqrt{2\cdot 7} + 2\cdot 2\cdot 2\sqrt{2\cdot 7} = ?\)

\(\displaystyle 12\sqrt{14} + 8 \sqrt{14} = ?\)

Now the numbers can be added directly because the expressions under the square roots match.

\(\displaystyle 12\sqrt{14} + 8\sqrt{14} = 20\sqrt{14}\)

First, we can simplify the radicals by factoring.

\(\displaystyle x\sqrt{96} + x\sqrt{150} = \sqrt{162}\)

\(\displaystyle x\sqrt{2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 3} + x\sqrt{2\cdot 3\cdot 5\cdot 5} = \sqrt{2\cdot 3\cdot 3\cdot 3\cdot 3}\)

\(\displaystyle x\left (2\cdot 2 \right )\sqrt{2\cdot 3} + x\left ( 5\right )\sqrt{2\cdot 3} = \left (3\cdot 3 \right )\sqrt{2}\)

\(\displaystyle 4x\sqrt{6} + 5x\sqrt{6} = 9\sqrt{2}\)

Now, we can factor out the \(\displaystyle x\).

\(\displaystyle x\left (4\sqrt{6} + 5\sqrt{6} \right ) = 9\sqrt{2}\)

\(\displaystyle x\left (9\sqrt{6} \right ) = 9\sqrt{2}\)

Now divide and simplify.

\(\displaystyle x = \frac{9\sqrt{2}}{9\sqrt{6} } = \frac{\sqrt{2}}{\sqrt{2\cdot 3}} = \frac{1}{\sqrt{3}}\)

To begin with, factor out the contents of the radicals.  This will make answering much easier:

\(\displaystyle \sqrt{210}+\sqrt{55}=\sqrt{2*3*5*7}+\sqrt{5*11}\)

They both have a common factor \(\displaystyle 5\).  This means that you could rewrite your equation like this:

\(\displaystyle \sqrt{5}\sqrt{2*3*7}+\sqrt{5}\sqrt{11}\)

This is the same as:

\(\displaystyle \sqrt{5}\sqrt{42}+\sqrt{5}\sqrt{11}\)

These have a common \(\displaystyle \sqrt{5}\).  Therefore, factor that out:

\(\displaystyle \sqrt{5}\sqrt{42}+\sqrt{5}\sqrt{11}=\sqrt{5}(\sqrt{42}+\sqrt{11})\)

These three roots all have a \(\displaystyle 5\) in common; therefore, you can rewrite them:

\(\displaystyle \sqrt{15}-\sqrt{20}+\sqrt{35}=\sqrt{3*5}-\sqrt{4*5}+\sqrt{7*5}\)

Now, this could be rewritten:

\(\displaystyle \sqrt{3*5}-\sqrt{4*5}+\sqrt{7*5}=\sqrt{5}\sqrt{3}-\sqrt{5}\sqrt{4}+\sqrt{5}\sqrt{7}\)

Now, note that \(\displaystyle \sqrt{4}=2\)

Therefore, you can simplify again:

\(\displaystyle \sqrt{5}\sqrt{3}-\sqrt{5}\sqrt{4}+\sqrt{5}\sqrt{7}=\sqrt{5}\sqrt{3}-2\sqrt{5}+\sqrt{5}\sqrt{7}\)

Now, that looks messy! Still, if you look carefully, you see that all of your factors have \(\displaystyle \sqrt{5}\); therefore, factor that out:

\(\displaystyle \sqrt{5}\sqrt{3}-2\sqrt{5}+\sqrt{5}\sqrt{7}=\sqrt{5}(\sqrt{3}-2+\sqrt{7})\)

This is the same as:

\(\displaystyle \sqrt{5}(\sqrt{3}+\sqrt{7}-2)\)

Begin by factoring out the relevant squared data:

\(\displaystyle x\sqrt{50}+x\sqrt{8}-\sqrt{18}+\sqrt{98}\) is the same as

\(\displaystyle x\sqrt{25*2}+x\sqrt{4*2}-\sqrt{9*2}+\sqrt{49*2}\)

This can be simplified to:

\(\displaystyle 5x\sqrt{2}+2x\sqrt{2}-3\sqrt{2}+7\sqrt{2}\)

Since your various factors contain square roots of \(\displaystyle 2\), you can simplify:

\(\displaystyle 7x\sqrt{2}+4\sqrt{2}\)

Technically, you can factor out a \(\displaystyle \sqrt{2}\):

\(\displaystyle \sqrt{2}(7x+4)\)