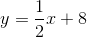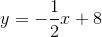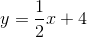The amplitude is half the measure from a trough to a peak.

The x-coordinate for the midpoint is given by taking the arithmetic average (mean) of the x-coordinates of the two end points. So the x-coordinate of the midpoint is given by \(\displaystyle (1+7)\div2=4\)

The same procedure is used for the y-coordinates. So the y-coordinate of the midpoint is given by \(\displaystyle (5+3)\div2=4\)

Thus the midpoint is given by the ordered pair \(\displaystyle (4, 4)\)

\(\displaystyle k\) is the \(\displaystyle y\)-intercept and equals \(\displaystyle 3\). \(\displaystyle n\) can be solved for by substituting \(\displaystyle 5\) in the equation for \(\displaystyle y\), which yields \(\displaystyle \frac{2}{7}\)

\(\displaystyle 3-\frac{2}{7}=\frac{21}{7}-\frac{2}{7}=\frac{19}{7}\)

Plug in \(\displaystyle 0\) for \(\displaystyle x\) to find a point on the line:

\(\displaystyle 3(0) + 2y = 6\)

\(\displaystyle y = 3\)

Thus, \(\displaystyle (0,3)\) is a point on the line.

Plug in \(\displaystyle 0\)  for \(\displaystyle y\) to find a second point on the line:

\(\displaystyle 3x + 2(0) = 6\)

\(\displaystyle x = 2\)

\(\displaystyle (2,0)\) is another point on the line.

Now we know that the line passes through the points \(\displaystyle (2,0)\) and \(\displaystyle (0,3)\).  

A quick sketch of the two points reveals that the line passes through all but the third quadrant.

First, we need to find the slope of the above line. 

The slope of a line. given two points \(\displaystyle (x_{1}, y_{1}), (x_{2}, y_{2})\) can be calculated using the slope formula

\(\displaystyle m = \frac{y_{2}-y_{1}}{x_{2}-x _{1}}\)

Set \(\displaystyle x_{1}=-4, y_{1}=x_{2}= 0, y_{2}=8\):

\(\displaystyle m = \frac{8-0}{0-(-4)} = \frac{8}{4} = 2\)

The slope of a line perpendicular to it has as its slope the opposite of the reciprocal of 2, which would be \(\displaystyle m = -\frac{1}{2}\). Since we want this line to have the same \(\displaystyle y\)-intercept as the first line, which is the point \(\displaystyle (0,8)\), we can substitute \(\displaystyle m = -\frac{1}{2}\) and \(\displaystyle b = 8\) in the slope-intercept form:

\(\displaystyle y = mx + b\)

\(\displaystyle y = - \frac{1}{2}x + 8\)

One way to answer this is to first find the equation of the line. 

The slope of a line. given two points \(\displaystyle (x_{1}, y_{1}), (x_{2}, y_{2})\) can be calculated using the slope formula

\(\displaystyle m = \frac{y_{2}-y_{1}}{x_{2}-x _{1}}\)

Set \(\displaystyle x_{1}=-6, y_{1}=x_{2}= 0, y_{2}=18\):

\(\displaystyle m = \frac{18-0}{0-(-6)} = \frac{18}{6} = 3\)

The line has slope 3 and \(\displaystyle y\)-intercept \(\displaystyle (0,18)\), so we can substitute \(\displaystyle m = 3, b = 18\) in the slope-intercept form:

\(\displaystyle y = mx+b\)

\(\displaystyle y = 3x+18\)

Now substitute 4 for \(\displaystyle y\) and \(\displaystyle N\) for \(\displaystyle x\) and solve for \(\displaystyle N\):

\(\displaystyle 4= 3N+18\)

\(\displaystyle -14 =3N\)

\(\displaystyle N = -\frac{14}{3}= -4\frac{2}{3}\)

When graphed, each equation is a parabola in the form of a quadratic. Quadratics have the form y = ax² + bx + c, where –b/2a = axis of symmetry. The maximum height is the vertex of each quadratic. Find the axis of symmetry, and plug that x-value into the equation to obtain the vertex.

To determine where an equation intercepts a given axis, input 0 for either \(\displaystyle x\) (where it intercepts the \(\displaystyle y\)-axis) or \(\displaystyle y\) (where it intercepts the \(\displaystyle x\)-axis), then solve. In this case, we want to know where the equation intercepts the \(\displaystyle x\)-axis; so we will plug in 0 for \(\displaystyle y\), giving:

\(\displaystyle y = x^{}2 ­­+ 7x + 12\)

\(\displaystyle 0 = x^{}2 ­­+ 7x + 12\)

Now solve for \(\displaystyle x\).

Note that in its present form, this is a quadratic equation. In this scenario, we must find two factors of 12, that when added together, equal 7. Quickly, we see that 4 and 3 fit these conditions, giving:

\(\displaystyle 0 = (x + 4)(x + 3)\)

Solving for \(\displaystyle x\), we see that there are two solutions,

\(\displaystyle x = -4\) or \(\displaystyle -3\)

The x intercept of an equation is the point at which it crosses the x-axis. To find the x intercept, plug in \(\displaystyle 0\) for \(\displaystyle y\) and solve for \(\displaystyle x\).

\(\displaystyle 0 = x^2 - 2x - 3\)

To solve for \(\displaystyle x\), we can factor the equation. We must find two numbers that add to equal \(\displaystyle -2\) and multiply to equal \(\displaystyle -3\). \(\displaystyle -3\) and \(\displaystyle 1\) fit these conditions, giving:

\(\displaystyle 0 = \left (x+1\right )\left ( x-3\right )\)

We can set each of these equal to \(\displaystyle 0\) to find two solutions for \(\displaystyle x\).

\(\displaystyle 0 = x-3\) and \(\displaystyle 0 = x+1\)

\(\displaystyle x=3, -1\)

The x intercepts occur at these \(\displaystyle x\) values, giving the coordinates:

\(\displaystyle \left ( 3, 0\right )\) and \(\displaystyle \left ( -1, 0\right )\)

The x intercept of an equation is the point at which it crosses the x-axis. To find the x intercept, plug in \(\displaystyle 0\) for \(\displaystyle y\) and solve for \(\displaystyle x\).

\(\displaystyle 0 = x^2 + 5x -9\)

This equation is not easily factored, so to solve for \(\displaystyle x\), we can use the quadratic formula:

\(\displaystyle x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)

With the equation in the form

\(\displaystyle y = ax^2 + bx + c\),

\(\displaystyle a = 1\), \(\displaystyle b = 5\), and \(\displaystyle c = -9\).

Plugging these values into the quadratic formula, we get:

\(\displaystyle x = \frac{-5 \pm \sqrt{5^2 - 4\left (1 \right )\left (-9 \right )}}{2\left (1 \right )} = \frac{-5 \pm \sqrt{61}}{2}\)

Find the two solutions for \(\displaystyle x\):

\(\displaystyle x = \frac{-5 + \sqrt{61}}{2} = 1.4\)

\(\displaystyle x = \frac{-5 - \sqrt{61}}{2} = -6.4\)

The x intercepts occur at these \(\displaystyle x\) values, giving the coordinates:

\(\displaystyle (1.4, 0)\) and \(\displaystyle \left (- 6.4, 0\right )\)