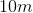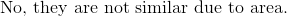We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : Plane Geometry

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Length Of The Side Of A Square

The circle that circumscribes Square SQUA has circumference 20. To the nearest tenth, evaluate .

Possible Answers:

2.3

4.5

3.2

6.4

9.0

Correct answer:

4.5

Explanation:

The diameter of a circle with circumference 20 is

$\frac{20}{\pi } \approx \frac{20 }{3.1416} \approx 6.3662$

The diameter of a circle that circumscribes a square is equal to the length of the diagonals of the square.

If diagonal $\overline{SU}$ of Square SQUA is constructed, then $\bigtriangleup SQU$ is a 45-45-90 triangle with hypotenuse approximately 6.3662. By the 45-45-90 Theorem, divide this by $\sqrt{2} \approx 1.4142$ to get the sidelength of the square:

$6.3662 \div 1.4142 \approx 4.5$

Report an Error

Example Question #1 : How To Find The Length Of The Side Of A Square

Rectangle RECT has area 90% of that of Square SQUA , and is 80% of . What percent of is ?

Possible Answers:

$112\frac{1}{2} \%$

$70 \%$

$79\frac{1}{81} \%$

$88 \frac{8} {9} \%$

$126 \frac{9}{16} \%$

Correct answer:

$88 \frac{8} {9} \%$

Explanation:

The area of Square SQUA is the square of sidelength , or $(SQ)^{2}$ .

The area of Rectangle RECT is $RE \cdot EC$ . Rectangle RECT has area 90% of that of Square SQUA , which is $\frac{9}{10} (SQ)^{2}$ ; is 80% of , so $RE = \frac{4}{5}SQ$ . We can set up the following equation:

$\frac{9}{10} (SQ)^{2} = RE \cdot EC$

$\frac{9}{10} (SQ)^{2} = \frac{4}{5} SQ \cdot EC$

$\frac{9}{10} \cdot SQ = \frac{4}{5} \cdot EC$

$\frac{10} {9} \cdot \frac{9}{10} \cdot SQ = \frac{10} {9} \cdot \frac{4}{5} \cdot EC$

$SQ = \frac{8} {9} \cdot EC$

As a percent, $\frac{8} {9}$ of is $\frac{8} {9} \times 100 \%= 88 \frac{8} {9} \%$

Report an Error

Example Question #22 : Squares

Reducing the area of a square by 12% has the effect of reducing its sidelength by what percent (hearest whole percent)?

Possible Answers:

$6 \%$

$15 \%$

$9 \%$

$3 \%$

$12 \%$

Correct answer:

$6 \%$

Explanation:

The area of the square was originally

$A = s^{2}$ ,

being the sidelength.

Reducing the area by 12% means that the new area is 88% of the original area, or 0.88A ; the square root of this is the new sidelength, so

$0.88A = 0.88s^{2}$

$\sqrt{0.88A} = \sqrt{0.88s^{2}} = \sqrt{0.88} \cdot \sqrt{s^{2}} \approx 0.94 s$

Each side of the new square will measure 94% of the length of the old measure - a reduction by 6%.

Report an Error

Example Question #411 : Geometry

The circle inscribed inside Square SQUA has circumference 16. To the nearest tenth, evaluate .

Possible Answers:

3.6

2.5

10.2

5.1

7.2

Correct answer:

5.1

Explanation:

The diameter of a circle that is inscribed inside a square is equal to its sidelength , so all we need to do is find the diameter of the circle - which is circumference 16 divided by $\pi$ :

$\frac{16}{\pi } \approx \frac{16}{3.1416 } \approx 5.1$ .

Report an Error

Example Question #171 : Quadrilaterals

Thingy

Refer to the above figure, which shows equilateral triangle $\bigtriangleup CDE$ inside Square ABCD . Also, $\overline{EF} \perp \overline{AB}$ .

Quadrilateral BCEF has area 100. Which of these choices comes closest to ?

Possible Answers:

Correct answer:

Explanation:

Let s = CD , the sidelength shared by the square and the equilateral triangle.

The area of $\bigtriangleup CDE$ is

$\frac{s^{2}\sqrt{3}}{4} = \frac{\sqrt{3}}{4} \cdot s^{2} \approx \frac{1.7321}{4} \cdot s^{2} \approx 0.4330 s^{2}$

The area of Square ABCD is $s^{2}$ .

By symmetry, $\overline{EF}$ bisects the portion of the square not in the triangle, so the area of Quadrilateral BCEF is half the difference of those of the square and the triangle. Since the area of Quadrilateral BCEF is 100, we can set up an equation:

$\frac{1}{2}\left (s ^{2} - 0.4330 s ^{2} \right ) = 100$

$\frac{1}{2}\left ( 0.5670 s ^{2} \right ) = 100$

$0.2835 s ^{2} = 100$

$s ^{2} \approx 100 \div 0.2835$

$s ^{2} \approx 352.73$

$s \approx\sqrt{ 352.73} \approx 18.7$

Of the five choices, 20 comes closest.

Report an Error

Example Question #411 : Geometry

Find the length of the side of a square given its area is 144 .

Possible Answers:

Correct answer:

Explanation:

To find side length, simply take the square root of the volume. Thus,

$s=\sqrt{V}=\sqrt{144}=12$

Report an Error

Example Question #1 : Other Quadrilaterals

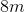
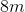
The sides of rectangle A measure to , , 12m , and 12m . Rectangle B is similar to Rectangle A. The shorter sides of rectangle B measure 10m each. How long are the longer sides of Rectangle B?

Possible Answers:

10m

16m

15m

14m

Correct answer:

15m

Explanation:

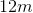
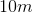
In similar rectangles, the ratio of the sides must be equal.

To solve this question, the following equation must be set up:

$\small \frac{8}{12}=\frac{10}{x}$ , using $\small x$ as the variable for the missing side.

We then must cross multiply, which leaves us with:

$\small 8x=120$

Lastly, we divide both sides by 8 to solve for the missing side:

$\small \frac{8x}{8}=\frac{120}{8}$

x=15

Therefore, the longer sides of the rectangle are each 15m .

Report an Error

Example Question #412 : Act Math

Suppose a rectangle has side lengths of 7 and 3. Another rectangle has another set of side lengths that are 8 and 4. Are these similar rectangles, and why?

Possible Answers:

$\textup{There is not enough information.}$

$\textup{Yes, dimensions are only one unit more than the lengths of the other rectangle.}$

$\textup{No, they are not similar due to proportion.}$

$\textup{No, they are not similar due to area.}$

$\textup{No, they are not similar due to length.}$

Correct answer:

$\textup{No, they are not similar due to proportion.}$

Explanation:

Set up the proportion to determine if the ratios of both rectangles are equal.

If they are, then they are similar.

$\frac{7}{3} =\frac{8}{4}?$

$\frac{7}{3} \neq 2$

These are not similar rectangles since their ratios are not the same.

Report an Error

Example Question #411 : Act Math

A square has a length of . What must be the length of the diagonal?

Possible Answers:

$3\sqrt{2x}$

$3\sqrt2$

$3x\sqrt2$

$9x\sqrt2$

$3x^2\sqrt2$

Correct answer:

$3x\sqrt2$

Explanation:

A square with a length of indicates that all sides are since a square has 4 equal sides. Use the Pythagorean Theorem to solve for the diagonal.

a^2+b^2=c^2

$c=\sqrt{a^2+b^2} = \sqrt{(3x)^2+(3x)^2}= \sqrt{9x^2+9x^2}= \sqrt{18x^2}= 3x\sqrt2$

Report an Error

Example Question #412 : Act Math

If the rectangle has side lengths of x+3 and x+4 , what is the diagonal of the rectangle?

Possible Answers:

$\sqrt{2x^2+5}$

$x+\frac{7}{3}$

$\sqrt{2x^2+14x+25}$

$\sqrt{x^2+7x+12}$

$\sqrt{2x^2+14x+24}$

Correct answer:

$\sqrt{2x^2+14x+25}$

Explanation:

Use the Pythagorean Theorem to solve for the diagonal.

a^2+b^2=c^2

(x+3)^2+(x+4)^2=c^2

c^2 = (x^2+6x+9) + (x^2+8x+16) = 2x^2+14x+25

$c=\sqrt{2x^2+14x+25}$

Report an Error

View ACT Math Tutors

Ann
Certified Tutor

Wright State University-Main Campus, Bachelor of Science, Mathematics and Computer Science. Western Governors University, Mas...

View ACT Math Tutors

Amit
Certified Tutor

The University of Texas at Austin, Bachelor of Science, Mathematics. The University of Texas at Dallas, Master of Science, Co...

View ACT Math Tutors

Ping
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Computer Science. University of North Texas, Master of Arts, Education.

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

SSAT Courses & Classes in Miami, ACT Courses & Classes in Phoenix, MCAT Courses & Classes in Atlanta, ACT Courses & Classes in Washington DC, SSAT Courses & Classes in Atlanta, ISEE Courses & Classes in Boston, ISEE Courses & Classes in Philadelphia, ISEE Courses & Classes in Phoenix, ISEE Courses & Classes in Washington DC, GMAT Courses & Classes in Houston

Popular Test Prep

GMAT Test Prep in San Francisco-Bay Area, GRE Test Prep in San Francisco-Bay Area, ISEE Test Prep in Washington DC, ISEE Test Prep in Boston, SAT Test Prep in Atlanta, SAT Test Prep in Los Angeles, LSAT Test Prep in Boston, GMAT Test Prep in Houston, ACT Test Prep in Washington DC, ACT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : Plane Geometry

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #1 : How To Find The Length Of The Side Of A Square

Example Question #1 : How To Find The Length Of The Side Of A Square

Example Question #22 : Squares

Example Question #411 : Geometry

Example Question #171 : Quadrilaterals

Example Question #411 : Geometry

Example Question #1 : Other Quadrilaterals

Example Question #412 : Act Math

Example Question #411 : Act Math

Example Question #412 : Act Math

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: