All ACT Math Resources
Example Questions
Example Question #141 : Geometry
Given a right triangle with a leg length of 2 and a hypotenuse length of √8, find the length of the other leg, x.

10
6
2
√8
4
2
Using Pythagorean Theorem, we can solve for the length of leg x:
x2 + 22 = (√8)2 = 8
Now we solve for x:
x2 + 4 = 8
x2 = 8 – 4
x2 = 4
x = 2
Example Question #2 : How To Find The Length Of The Side Of A Right Triangle
The legs of a right triangle are 

Use the Pythagorean Theorem. The sum of both legs squared equals the hypotenuse squared.
Example Question #81 : Triangles
Find the length of segment 
The length of segment 
Note that triangles 






which simplifies to 
Example Question #1 : How To Find The Length Of The Side Of A Right Triangle
A handicap ramp is 

In this case, we are already given the length of the hypotenuse of the right triangle, but the Pythagorean formula still helps us. Plug and play, remembering that 



Thus, the ramp covers 
Example Question #81 : Triangles
You have two right triangles that are similar. The base of the first is 6 and the height is 9. If the base of the second triangle is 20, what is the height of the second triangle?
25
33
30
23
35
30
Similar triangles are proportional.
Base1 / Height1 = Base2 / Height2
6 / 9 = 20 / Height2
Cross multiply and solve for Height2
6 / 9 = 20 / Height2
6 * Height2= 20 * 9
Height2= 30
Example Question #1 : Right Triangles
A right triangle is defined by the points (1, 1), (1, 5), and (4, 1). The triangle's sides are enlarged by a factor of 3 to form a new triangle. What is the area of the new triangle?
108 square units
54 square units
36 square units
None of the answers are correct
81 square units
54 square units
The points define a 3-4-5 right triangle. Its area is A = 1/2bh = ½(3)(4) = 6. The scale factor (SF) of the new triangle is 3. The area of the new triangle is given by Anew = (SF)2 x (Aold) =
32 x 6 = 9 x 6 = 54 square units (since the units are not given in the original problem).
NOTE: For a volume problem: Vnew = (SF)3 x (Vold).
Example Question #1 : How To Find If Right Triangles Are Similar
On a flat street, a light pole 36 feet tall casts a shadow that is 9 feet long. At the same time of day, a nearby light pole casts a shadow that is 6 feet long. How many feet tall is the second light pole?
Start by drawing out the light poles and their shadows.

In this case, we end up with two similar triangles. We know that these are similar triangles because the question tells us that these poles are on a flat surface, meaning angle B and angle E are both right angles. Then, because the question states that the shadow cast by both poles are at the same time of day, we know that angles C and F are equivalent. As a result, angles A and D must also be equivalent.
Since these are similar triangles, we can set up proportions for the corresponding sides.
Now, solve for 
Example Question #1 : Equilateral Triangles
What is the perimeter of an equilateral triangle with an area of 
Recall that from any vertex of an equilateral triangle, you can drop a height that is a bisector of that vertex as well as a bisector of the correlative side. This gives you the following figure:

Notice that the small triangles within the larger triangle are both 

The ratio of the small base to the height is the same as 
This means that 
Now, the area of a triangle can be written:



Now, let's write that a bit more simply:
Solve for 

Divide each side by 
Finally, take the square root of both sides. This gives you 

Example Question #1 : Equilateral Triangles
An equilateral triangle with a perimeter of 
An equilateral triangle has 3 equal length sides.
Therefore the perimeter equation is as follows,

So divide the perimeter by 3 to find the length of each side.
Thus the answer is:
Example Question #3 : Equilateral Triangles
Jill has an equilateral triangular garden with a base of 

Since the triangle is equilateral, the base and the legs are equal, so the first step is to set the two equations equal to each other. Start with 












All ACT Math Resources

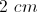





 ,
,  , and
, and  are collinear (they lie along the same line).
are collinear (they lie along the same line).  ,
,  ,
,  ,
, 















































