All ACT Math Resources
Example Questions
Example Question #11 : Clock Math
What is the angle of the minor arc between the minute and hour hands of a clock reading 

To find angular distance between the minute and hour hand, first find the position of each. Using 
First, remember that a circle contains 

For the hour hand, each hour in a 12-hour cycle takes up 

Thus, our distance from 


Likewise, our distance from 


Then, all we need to do is find the positive difference between these two measurements, 
This looks more complicated than it is! Fortunately, once our equation is set up, the problem is as easy as plug and play. First, let's find the measure of the minor arc between the minute hand and the reference. We can ignore hours (as each hour returns the minute hand to our reference angle) and just look at minutes.
Now, find the same distance, but for the hour hand. Here, we must consider both hours and minutes by using a fraction:
Lastly, we find the difference between these two references (remembering that our answer should be positive):
Thus, the hands are 

Example Question #13 : How To Find The Angle Of Clock Hands
What is the angle of the minor arc between the minute and hour hands of a clock reading 

To find angular distance between the minute and hour hand, first find the position of each. Using 
First, remember that a circle contains 

For the hour hand, each hour in a 12-hour cycle takes up 

Thus, our distance from 


Likewise, our distance from 


Then, all we need to do is find the positive difference between these two measurements, 
This looks more complicated than it is! Fortunately, once our equation is set up, the problem is as easy as plug and play. First, let's find the measure of the minor arc between the minute hand and the reference. We can ignore hours (as each hour returns the minute hand to our reference angle) and just look at minutes.
Now, find the same distance, but for the hour hand. Here, we must consider both hours and minutes by using a fraction:
Lastly, we find the difference between these two references (remembering that our answer should be positive):
Thus, the hands are 

Example Question #14 : How To Find The Angle Of Clock Hands
What is the angle of the major arc between the minute and hour hands of a clock reading 

To find angular distance between the minute and hour hand, first find the position of each. Using 
First, remember that a circle contains 

For the hour hand, each hour in a 12-hour cycle takes up 

Thus, our distance from 


Likewise, our distance from 


Then, all we need to do is find the positive difference between these two measurements, 
This looks more complicated than it is! Fortunately, once our equation is set up, the problem is as easy as plug and play. First, let's find the measure of the minor arc between the minute hand and the reference. We can ignore hours (as each hour returns the minute hand to our reference angle) and just look at minutes.
Now, find the same distance, but for the hour hand. Here, we must consider both hours and minutes by using a fraction:
Lastly, we find the difference between these two references (remembering that our answer should be positive):
The problem asked for the major arc, so our answer is actually
Thus, the hands are 

Example Question #15 : How To Find The Angle Of Clock Hands
What is the angle of the major arc between the minute and hour hands of a clock reading 

To find angular distance between the minute and hour hand, first find the position of each. Using 
First, remember that a circle contains 

For the hour hand, each hour in a 12-hour cycle takes up 

Thus, our distance from 


Likewise, our distance from 


Then, all we need to do is find the positive difference between these two measurements, 
This looks more complicated than it is! Fortunately, once our equation is set up, the problem is as easy as plug and play. First, let's find the measure of the minor arc between the minute hand and the reference. We can ignore hours (as each hour returns the minute hand to our reference angle) and just look at minutes.
Now, find the same distance, but for the hour hand. Here, we must consider both hours and minutes by using a fraction:
Lastly, we find the difference between these two references (remembering that our answer should be positive):
Thus, the hands are 

Example Question #16 : How To Find The Angle Of Clock Hands
What is the angle of the major arc between the minute and hour hands of a clock reading 

To find angular distance between the minute and hour hand, first find the position of each. Using 
First, remember that a circle contains 

For the hour hand, each hour in a 12-hour cycle takes up 

Thus, our distance from 


Likewise, our distance from 


Then, all we need to do is find the positive difference between these two measurements, 
This looks more complicated than it is! Fortunately, once our equation is set up, the problem is as easy as plug and play. First, let's find the measure of the minor arc between the minute hand and the reference. We can ignore hours (as each hour returns the minute hand to our reference angle) and just look at minutes.
Now, find the same distance, but for the hour hand. Here, we must consider both hours and minutes by using a fraction:
Lastly, we find the difference between these two references (remembering that our answer should be positive):
The problem asked for the major arc, so our answer is actually
Thus, the hands are 

Example Question #17 : How To Find The Angle Of Clock Hands
A watch's hands move from 

First, remember that a circle contains 

Thus, our total distance from our reference angle can be found as 

In this case, we simply find the difference of the two times, remembering to first convert hours to minutes:
Now, plug our answer in minutes into our equation:
So, our minute hand has moved 
Example Question #18 : How To Find The Angle Of Clock Hands
A watch's hands move from 

First, remember that a circle contains 

Thus, our total distance from our reference angle can be found as 

In this case, we simply find the difference of the two times, remembering to first convert hours to minutes:
Now, plug our answer in minutes into our equation:
So, our minute hand has moved 
Example Question #19 : How To Find The Angle Of Clock Hands
A watch's hands move from 

First, remember that an hour hand moves 

Thus, our total distance from our reference angle can be found as 

In this case, we simply find the difference of the two times, remembering to first convert hours to minutes:
Now, plug our answer in minutes into our equation:
So, our hour hand has moved 
Example Question #20 : How To Find The Angle Of Clock Hands
A clock reads 
When the clock reads 



Since there are 
Alternatively, if the clock reads 



Example Question #31 : Circles
On a standard analog clock, what is the angle between the hands when the clock reads 
To find the degrees of a clock hand, first find the angle between each hour-long sections. Since there are 







There are 
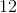


All ACT Math Resources














































































