All ACT Math Resources
Example Questions
Example Question #1 : How To Find The Length Of The Diagonal Of A Parallelogram
If a rectangular plot measures 

To answer this question, we must find the diagonal of a rectangle that is 

Because a right triangle is formed by the diagonal, we can use the Pythagorean Theorem, which is:



We can then plug in our known values and solve for
We now must take the square root of each side so that we can solve for
Therefore, the diagonal of the rectangle is 
Example Question #331 : Geometry
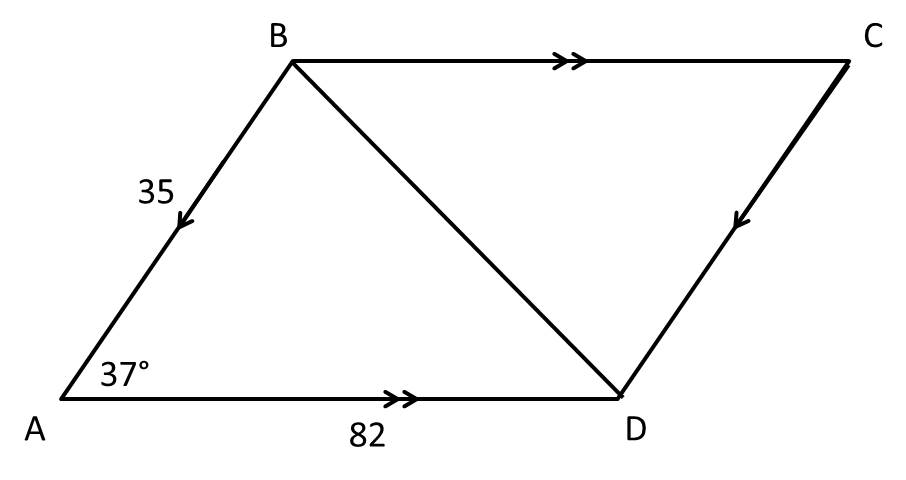


To find the length of the diagonal, we can consider only the triangle 
The Law of Cosines:
Where 





From the problem:
Example Question #2 : How To Find The Length Of The Diagonal Of A Parallelogram



To find the length of the diagonal, we can consider only the triangle 
The Law of Cosines:
Where 





From the problem:
Example Question #3 : How To Find The Length Of The Diagonal Of A Parallelogram



To find the length of the diagonal, we can consider only the triangle 
The Law of Cosines:
Where 





From the problem:
Example Question #4 : How To Find The Length Of The Diagonal Of A Parallelogram



To find the length of the diagonal, we can consider only the triangle 
The Law of Cosines:
Where 





From the problem:
Example Question #5 : How To Find The Length Of The Diagonal Of A Parallelogram



To find the length of the diagonal, we can consider only the triangle 
The Law of Cosines:
Where 





From the problem:
Example Question #6 : How To Find The Length Of The Diagonal Of A Parallelogram



To find the length of the diagonal, we can consider only the triangle 
The Law of Cosines:
Where 





From the problem:
All ACT Math Resources


































































