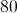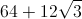All ACT Math Resources
Example Questions
Example Question #1 : How To Find The Perimeter Of A Parallelogram
A parallelogram, with dimensions in cm, is shown below.
What is the perimeter of the parallelogram, in cm?
The triangle on the left side of the figure has a 


Our third angle is 

A 



We also now know that
Now we know all of our missing side lengths. The right and left side of the parallelogram will each be 

Example Question #321 : Geometry

Note: Figure NOT drawn to scale.
Give the perimeter of Parallelogram 
By the 30-60-90 Theorem, the length of the short leg of 

Its hypotenuse has twice the length of the short leg, so
The perimeter of the parallelogram is
Example Question #1 : How To Find The Perimeter Of A Parallelogram

Note: Figure NOT drawn to scale.
Give the perimeter of Parallelogram 
By the 45-45-90 Theorem, the lengths of the legs of 
Its hypotenuse has measure 
The perimeter of the parallelogram is
Example Question #332 : Geometry

Note: Figure NOT drawn to scale.
To the nearest tenth, give the perimeter of Parallelogram 
The perimeter of the parallelogram is
Example Question #2 : How To Find The Perimeter Of A Parallelogram

In the above figure, Parallelogram 
By the 45-45-90 Theorem, 


Also by the 45-45-90 Theorem,
The perimeter of the parallelogram is
Example Question #334 : Geometry

In the above figure, Parallelogram 
By the 30-60-90 Theorem,
The area of the parallelogram is the product of height 

Also by the 30-60-90 Theorem,
The perimeter of the parallelogram is
Example Question #335 : Geometry

Note: Figure NOT drawn to scale.
In the above figure, Parallelogram 
The area of the parallelogram is the product of height 

The perimeter of the parallelogram is
All ACT Math Resources