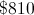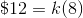The general formula for direct proportionality is

\(\displaystyle a=kb\)

where \(\displaystyle k\) is the proportionality constant. To find the value of this \(\displaystyle k\), we plug in \(\displaystyle a=24\) and \(\displaystyle b=12\)

\(\displaystyle 24=12k\)

Solve for \(\displaystyle k\) by dividing both sides by 12

\(\displaystyle \frac{24}{12}=\frac{12k}{12}\)

\(\displaystyle 2=k\)

So \(\displaystyle k=2\).

The general formula for direct proportionality is 

\(\displaystyle M=kh\)

where \(\displaystyle M\) is how much money you earned, \(\displaystyle k\) is the proportionality constant, and \(\displaystyle h\) is the number of hours worked.

Before we can figure out how many hours you need to work to earn $48, we need to find the value of \(\displaystyle k\). It is given that you earned $32 by working 4 hours. Plug these values into the formula

\(\displaystyle 32=4k\)

Solve for \(\displaystyle k\) by dividing both sides by 4.

\(\displaystyle \frac{32}{4}=\frac{4k}{4}\)

\(\displaystyle 8=k\)

So \(\displaystyle k=8\). We can use this to find out the hours you need to work to earn $48. With \(\displaystyle k=8\), we have

\(\displaystyle M=8h\)

Plug in $48.

\(\displaystyle 48=8h\)

Divide both sides by 8

\(\displaystyle \frac{48}{8}=\frac{8h}{8}\)

\(\displaystyle 6=h\)

So you will need to work 6 hours to earn $48.

If \(\displaystyle V,P,T\) are the volume, pressure, and temperature, then the variation equation will be, for some constant of variation \(\displaystyle K\),

\(\displaystyle V = \frac{KT}{P}\)

To calculate \(\displaystyle K\), substitute \(\displaystyle V = 100, T = 310, P = 1,020\):

\(\displaystyle 100 = \frac{K \cdot 310}{1,020}\)

\(\displaystyle \frac{K \cdot 310}{1,020} \cdot \frac{1,020}{310} = 100 \cdot \frac{1,020}{310}\)

\(\displaystyle K = 329.03\)

The variation equation is 

\(\displaystyle V = \frac{329.03 T}{P}\)

so substitute \(\displaystyle T =290, P = 900\) and solve for \(\displaystyle V\). 

\(\displaystyle V = \frac{329.03 \cdot 290}{900} \approx 106 \textrm{ m}^{3}\)

The statement, 'The monthly costly to insure your cars varies directly with the number of cars you own' can be mathematically expressed as \(\displaystyle M=kC\). M is the monthly cost, C is the number of cars owned, and k is the constant of variation.

Given that it costs $420 a month to insure 3 cars, we can find the k-value.

\(\displaystyle 420=k * 3\)

Divide both sides by 3.

\(\displaystyle k=140\)

Now, we have the mathematical relationship.

\(\displaystyle M=140C\)

Finding how much it costs to insure 5 cars can be found by substituting 5 for C and solving for M.

\(\displaystyle M=140(5)\)

\(\displaystyle M=700\)

Direct Variation is a relationship that can be represented by a function in the form

\(\displaystyle y = kx\), where \(\displaystyle k \neq 0\)

\(\displaystyle k\) is the constant of variation for a direct variation. \(\displaystyle k\) is the coefficient of \(\displaystyle x\).

\(\displaystyle 7y = 2x\)

\(\displaystyle y = \frac{2}{7}x\)

The equation is in the form \(\displaystyle y = kx\), so the equation is a direct variation.

The constant of variation or \(\displaystyle k\) is \(\displaystyle \frac{2}{7}\)

Therefore, the answer is,

Yes it is a direct variation, \(\displaystyle y = \frac{2}{7}x,\) with a direct variation of \(\displaystyle \frac{2}{7}\)

The general formula for direct proportionality is

\(\displaystyle x=ky\)

where \(\displaystyle k\) is our constant of proportionality. From here we can plug in the relevant values for \(\displaystyle x\) and \(\displaystyle y\) to get

\(\displaystyle 24=4k\)

Solving for \(\displaystyle k\) requires that we divide both sides of the equation by \(\displaystyle 4\), yielding

\(\displaystyle k=6\)

Because the cost varies directly with the number of people attending, we have the equation

\(\displaystyle C=kN\)

Where \(\displaystyle C\) is the cost and \(\displaystyle N\) is the number of people attending. 

We solve for \(\displaystyle k\), the constant of variation, by plugging in \(\displaystyle C=100\) and \(\displaystyle N=20\).

\(\displaystyle 100=k(20)\)

And by dividing by 20 on both sides

\(\displaystyle \frac{100}{20}=\frac{k(20) }{20}\)

Yields

\(\displaystyle k=5\)

Write the formula for direct proportionality.

\(\displaystyle y=kx\)

Let:

\(\displaystyle x=\textup{hours worked}\)

\(\displaystyle y= \textup{earnings}\)

Substitute twelve dollars and eight hours into this equation to solve for \(\displaystyle k\).

\(\displaystyle \$12=k(8)\)

Divide by eight on both sides.

\(\displaystyle k=\frac{12}{8} = \frac{3}{2}\)

Substitute \(\displaystyle k\) back into the formula.

\(\displaystyle y=\frac{3}{2}x\)

To find out the minimum number of hours Billy must work to make \(\displaystyle \$100\), substitute \(\displaystyle \$100\) into \(\displaystyle y\) and solve for \(\displaystyle x\).

\(\displaystyle \$100=\frac{3}{2}x\)

Multiply by two thirds on both sides.

\(\displaystyle 100\cdot \frac{2}{3}=\frac{3}{2}x \cdot \frac{2}{3}\)

Simplify both sides.

\(\displaystyle x=\frac{200}{3} = 66.\overline{6}\)

Billy must work at least \(\displaystyle 67\) hours to earn as much required.

\(\displaystyle f\left ( x \right ) = x^{2}-3\)

which is the same as

\(\displaystyle y = x^{2}-3\)

If we solve for \(\displaystyle x\) we get

\(\displaystyle x^{2} = y +3\)

Taking the square root of both sides gives us the following:

\(\displaystyle x = \pm \sqrt{y+3}\)

Interchanging \(\displaystyle x\) and \(\displaystyle y\) gives us

\(\displaystyle y = \pm \sqrt{x + 3}\)

Which is not one-to-one and therefore not a function.

Starting with \(\displaystyle f\left ( x \right ) = 2x+3\)

Replace \(\displaystyle x\) with \(\displaystyle g\left ( x \right )\).

We get the following:

\(\displaystyle 2\left ( \frac{x-3}{2} \right )+3=x-3+3\)

Which is equal to \(\displaystyle x\).