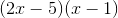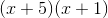To factor the trinomial, its general form given by \(\displaystyle ax^2+bx+c\), we must find factors of the product \(\displaystyle a\cdot c\) that when added together give us \(\displaystyle b\). 

For our trinomial, \(\displaystyle a\cdot c= 10\) and \(\displaystyle b=7\). The two factors that fit the above rule are \(\displaystyle 5\) and \(\displaystyle 2\), because \(\displaystyle 5\cdot2=10=a\cdot c\) and \(\displaystyle 5+2=7=b\).

Using the two factors, we can rewrite the term \(\displaystyle bx\) as a sum of the two factors added together and multiplied by x:

\(\displaystyle 2x^2+2x+5x+5\)

Now, we must factor by grouping, which means we group the first two terms, and the last two terms, and factor them:

\(\displaystyle 2x(x+1)+5(x+1)\)

Note that after we factored the two groups of terms, what remained inside the parentheses is identical for the two groups.

Simplifying further, we get

\(\displaystyle (2x+5)(x+1)\), which is our final answer. 

A perfect square trinomial takes the form

\(\displaystyle x^{2}+ bx + c\),

where \(\displaystyle c= \left ( \frac{b}{2} \right )^{2}\)

Since \(\displaystyle b = 22\), for \(\displaystyle x^{2}+ bx + c\) to be a perfect square, 

\(\displaystyle c= \left ( \frac{22}{2} \right )^{2} = 11^{2} = 121\).

This makes \(\displaystyle x^{2} + 22x + 121\) the correct choice.

Set up this problem vertically like you would a normal multiplication problem without variables. Then, multiply the \(\displaystyle -4\) term to each term in the trinomial. Next, multiply the \(\displaystyle 3x\) term to each term in the trinomial (keep in mind your placeholder!).

Then combine the two, which yields:

\(\displaystyle 12x^3-31x^2+47x-36\)

You can look at this as the sum of two expressions multiplied by the difference of the same two expressions. Use the pattern

\(\displaystyle \small (A+B)(A-B) = (A^{2}-B^{2})\),

where \(\displaystyle \small A = x^{2} - 2x\) and \(\displaystyle \small B = 7\).

\(\displaystyle \small \small \small (x^{2} - 2x + 7) (x^{2} - 2x - 7) = (x^{2} - 2x )^{2} - 7^{2} = (x^{2} - 2x )^{2} - 49\) 

To find \(\displaystyle \small (x^{2} - 2x )^{2}\), you use the formula for perfect squares:

\(\displaystyle \small (A-B)^{2} = (A^{2}-2AB+B^{2})\) ,

where \(\displaystyle \small \small A = x^{2}\) and \(\displaystyle \small B = 2x\).

\(\displaystyle \small \small \small (x^{2}-2x)^{2} = ((x^{2})^{2}-2x^{2}(2x)+(2x)^{2}) = x^{4}-4x^{3}+4x^2\)

Substituting above, the final answer is \(\displaystyle \small x^{4}-4x^{3}+4x^2-49\) .

When multiplying these two trinomials, you'll need to use a modified form of FOIL, by which every term in the first trinomial gets multiplied by every term in the second trinomial. One way to do this is to use the grid method.

You can also solve it piece by piece the way it is set up. First, multiply each of the three terms in the first trinomail by \(\displaystyle x^2\). Second, multiply each of those three terms again, this time by \(\displaystyle 3x\). Finally multiply the three terms again by \(\displaystyle -8\).

\(\displaystyle (2x^2-4x+7) \times x^2 = 2x^4 - 4x^3 + 7x^2\)

\(\displaystyle (2x^2-4x+7) \times 3x = 6x^3 - 12x^2 + 21x\)

\(\displaystyle (2x^2-4x+7) \times -8 = -16x^2 + 32x - 56\)

Finally, you can combine like terms after this multiplication to get your final simplified answer:

\(\displaystyle 2x^4+2x^3-21x^2+53x-56\)

When multiplying this trinomial by this binomial, you'll need to use a modified form of FOIL, by which every term in the binomial gets multiplied by every term in the trinomial. One way to do this is to use the grid method.

You can also solve it piece-by-piece the way it is set up. First, multiply each of the three terms in the trinomail by \(\displaystyle 2x\). Then multiply each of those three terms again, this time by \(\displaystyle 5\).

\(\displaystyle (x^2+2x-4) \times 2x = 2x^3 + 4x^2 - 8x\)

\(\displaystyle (x^2+2x-4) \times 5 = 5x^2 + 10x - 20\)

Finally, you can combine like terms after this multiplication to get your final simplified answer:

\(\displaystyle 2x^3 + 9x^2 +2x-20\)

Solving this is just like using FOIL on binomials, except we have nine calculations to perform instead of four (since that's the result of a 3x3 combination!):

First, calculate the combinations of the first term on the left:

\(\displaystyle (2x^2)(x^2 + x + 4) = 2x^4 + 2x^3 + 8x^2\)

Next, calculate the combinations of the middle term on the left:

\(\displaystyle (-3x)(x^2 + x + 4) = -3x^3 - 3x^2 - 12x\)

Next, calculate the combinations of the third term on the left:

\(\displaystyle (7)(x^2 + x + 4) = 7x^2 + 7x + 28\)

Lastly, combine the terms with compatible variables and exponents:

\(\displaystyle 2x^4 + 2x^3 + 8x^2 -3x^3 - 3x^2 - 12x +7x^2 + 7x + 28 = 2x^4 -x^3 + 12x^2 - 5x + 28\)

Thus, our answer is \(\displaystyle 2x^4 -x^3 + 12x^2 - 5x + 28\).

To solve this problem, first FOIL the binomial.

FOIL stands for the multiplication between the first terms, outer terms, inner terms, and then the last terms.

\(\displaystyle (x+3)^2 = x^2 + 6x + 9\)

Now, distribute the trinomials. Start with the first term on the left:

\(\displaystyle (x^2)(x^2 -4x - 4) = x^4 -4x^3 -4x^2\)

Now the middle term on the left:

\(\displaystyle (6x)(x^2 -4x - 4) = 6x^3 -24x^2 -24x\)

Now, the third term on the left:

\(\displaystyle (9)(x^2 -4x - 4) = 9x^2 -36x -36\)

Combine all compatible terms:
\(\displaystyle x^4 -4x^3 -4x^2 + 6x^3 -24x^2 -24x + 9x^2 -36x -36 = x^4 + 2x^3 -19x^2 -60x -36\)

Thus, \(\displaystyle x^4 + 2x^3 -19x^2 -60x -36\) is our answer.

The easy way to perform this calculation (without using Pascal's Triangle) is to find \(\displaystyle (x+6)^2\), then square that trinomial.

\(\displaystyle (x+6)^2 = x^2 + 12x + 36\)

So, our problem becomes

\(\displaystyle (x+6)^4 = (x^2 + 12x + 36)(x^2 + 12x + 36)\)

Start by distributing the first term on the left:

\(\displaystyle (x^2)(x^2 + 12x + 36) = x^4 + 12x^3 + 36x^2\)

Now distribute the second term on the left:

\(\displaystyle (12x)(x^2 + 12x + 36) = 12x^3 + 144x^2 + 432x\)

Now distribute the third term on the left:

\(\displaystyle (36)(x^2 + 12x + 36) = 36x^2 + 432x + 1296\)

Now, combine the compatible terms:

\(\displaystyle (x^2 + 12x + 36)(x^2 + 12x + 36) = x^4 + 24x^3 + 216x^2 + 864x + 1296\)

Thus, our answer is \(\displaystyle x^4 + 24x^3 + 216x^2 + 864x + 1296\).

We are asked to expand and simplify the expression: \(\displaystyle (2x+3y)^{-3}\).

This question is going to require knowledge of exponent rules and FOIL methods.

The first step is to create an inverse reciprocal of a negative exponent.

\(\displaystyle \frac{1}{(2x+3y)^{3}}\)

Now, we can expand the expression by removing the exponent in the denominator.

\(\displaystyle \frac{1}{(2x+3y)(2x+3y)(2x+3y)}\)

Use the FOIL method to first multiply \(\displaystyle (2x+3y)\) and \(\displaystyle (2x+3y)\).

\(\displaystyle (2x+3y)(2x+3y)= 4x^2+6xy+6xy+9y^2= 4x^2+12xy+9y^2\)

You'll find it creates \(\displaystyle 4x^2+12xy+9y^2\). Replace it back into the expression because we have to multiply the result by \(\displaystyle (2x+3y)\) one more time.

\(\displaystyle \frac{1}{(4x^2+12xy+9y^2)(2x+3y)}\)

Be careful with exponents and coefficients!

\(\displaystyle \frac{1}{8x^3+12{\color{DarkOrange} x^2y}+24{\color{DarkOrange} x^2y}+36{\color{Magenta} xy^2}+18{\color{Magenta} xy^2}+27y^3}\)

Combine like terms to find the simplified answer.

\(\displaystyle \frac{1}{8x^3+36x^2y+54xy^2+27y^3}\)