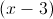Call Now to Set Up Tutoring:

(888) 888-0446

Algebra 1 : Variables

Study concepts, example questions & explanations for Algebra 1

Create An Account

All Algebra 1 Resources

10 Diagnostic Tests 557 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Solution To A Binomial Problem

Solve for $\displaystyle x$ in terms of $\displaystyle y$ :

$\frac{4}{3}x-3=\frac{2}{9}y$ $\displaystyle \frac{4}{3}x-3=\frac{2}{9}y$

Possible Answers:

$x=\frac{8}{27}y+3$ $\displaystyle x=\frac{8}{27}y+3$

$x=\frac{1}{6}y-\frac{9}{4}$ $\displaystyle x=\frac{1}{6}y-\frac{9}{4}$

$x=\frac{-8}{27}y+3$ $\displaystyle x=\frac{-8}{27}y+3$

$x=\frac{8}{27}y-3$ $\displaystyle x=\frac{8}{27}y-3$

$x=\frac{1}{6}y+\frac{9}{4}$ $\displaystyle x=\frac{1}{6}y+\frac{9}{4}$

Correct answer:

$x=\frac{1}{6}y+\frac{9}{4}$ $\displaystyle x=\frac{1}{6}y+\frac{9}{4}$

Explanation:

First, isolate X onto one side of the equation:

$\frac{4}{3}X-3=\frac{2}{9}Y$ $\displaystyle \frac{4}{3}X-3=\frac{2}{9}Y$

$\displaystyle +3$ $\displaystyle +3$

$\frac{4}{3}X=\frac{2}{9}Y+3$ $\displaystyle \frac{4}{3}X=\frac{2}{9}Y+3$

Next, divide both sides of the equation by 4/3:

$\frac{4}{3}\div \frac{4}{3}X=\frac{4}{3}\div \frac{2}{9}Y+\frac{4}{3}\div \frac{3}{1}$ $\displaystyle \frac{4}{3}\div \frac{4}{3}X=\frac{4}{3}\div \frac{2}{9}Y+\frac{4}{3}\div \frac{3}{1}$

$\frac{3}{4}\cdot \frac{4}{3}X=\frac{3}{4}\cdot \frac{2}{9}Y+\frac{3}{4}\cdot \frac{3}{1}$ $\displaystyle \frac{3}{4}\cdot \frac{4}{3}X=\frac{3}{4}\cdot \frac{2}{9}Y+\frac{3}{4}\cdot \frac{3}{1}$

$X=\frac{6}{36}Y+\frac{9}{4}$ $\displaystyle X=\frac{6}{36}Y+\frac{9}{4}$

When simplified, your answer should be:

$X=\frac{1}{6}Y+\frac{9}{4}$ $\displaystyle X=\frac{1}{6}Y+\frac{9}{4}$

Report an Error

Example Question #1 : How To Find The Solution To A Binomial Problem

Solve for $\displaystyle x$

$\displaystyle -1 = 6 + x$

Possible Answers:

$\displaystyle -7$

$\displaystyle 7$

$\displaystyle -5$

$\displaystyle 0$

$\displaystyle 5$

Correct answer:

$\displaystyle -7$

Explanation:

$\displaystyle -1 = 6 + x$

$\displaystyle -1-6 = 6+x-6$

-7 = x $\displaystyle -7 = x$

Report an Error

Example Question #1 : How To Find The Solution To A Binomial Problem

Solve for $\displaystyle x$

$\displaystyle 3 = -6 + x$

Possible Answers:

$\displaystyle 3$

$\displaystyle -2$

$\displaystyle -3$

$\displaystyle 9$

$\displaystyle -9$

Correct answer:

$\displaystyle 9$

Explanation:

$\\3 = -6 + x \\3 + 6 = -6 + x + 6 \\9 = x$ $\displaystyle \\3 = -6 + x \\3 + 6 = -6 + x + 6 \\9 = x$

Report an Error

Example Question #2 : How To Find The Solution To A Binomial Problem

Solve for $\displaystyle x$

$\displaystyle 3 = 2 - x$

Possible Answers:

$\displaystyle -1$

None of the other answers.

$\displaystyle 5$

$\displaystyle -5$

$\displaystyle 1$

Correct answer:

$\displaystyle -1$

Explanation:

$\\3 = 2 - x \\3 - 2 = 2 - x - 2\\ 1 = -x(-1) = x$ $\displaystyle \\3 = 2 - x \\3 - 2 = 2 - x - 2\\ 1 = -x(-1) = x$

Report an Error

Example Question #3 : How To Find The Solution To A Binomial Problem

Solve for $\displaystyle x$

$\displaystyle 19 = 7 + x$

Possible Answers:

$\displaystyle -26$

$\displaystyle 12$

$\displaystyle -12$

$\displaystyle 26$

$\displaystyle 7$

Correct answer:

$\displaystyle 12$

Explanation:

$\\19 = 7 + x \\ 19 - 7 = 7 + x -7 \\ 12 = x$ $\displaystyle \\19 = 7 + x \\ 19 - 7 = 7 + x -7 \\ 12 = x$

Report an Error

Example Question #301 : Variables

Solve for $\displaystyle x.$

$\displaystyle -9 = 82 + x$

Possible Answers:

$\displaystyle -91$

$\displaystyle 91$

None of the other answers.

$\displaystyle 72$

$\displaystyle 73$

Correct answer:

$\displaystyle -91$

Explanation:

$\\-9 = 82 + x \\ -9 - 82 = 82 + x - 82 \\-91 = x$ $\displaystyle \\-9 = 82 + x \\ -9 - 82 = 82 + x - 82 \\-91 = x$

Report an Error

Example Question #302 : Variables

Solve for $\displaystyle x$

$\displaystyle 1 = -3 + x$

Possible Answers:

$\displaystyle 1$

$\displaystyle 4$

$\displaystyle 3$

None of the other answers.

$\displaystyle 0$

Correct answer:

$\displaystyle 4$

Explanation:

$\\1 = -3 + x \\1 + 3 = -3 + x + 3\\ 4 = x$ $\displaystyle \\1 = -3 + x \\1 + 3 = -3 + x + 3\\ 4 = x$

Report an Error

Example Question #2 : Solving Rational Expressions

Simplify:

$\frac{2x-3}{3-2x}$ $\displaystyle \frac{2x-3}{3-2x}$

Possible Answers:

$\displaystyle 1$

$\frac{3}{2}$ $\displaystyle \frac{3}{2}$

$\frac{2}{3}$ $\displaystyle \frac{2}{3}$

$\displaystyle 0$

$\displaystyle -1$

Correct answer:

$\displaystyle -1$

Explanation:

Factor out $\displaystyle -1$ from the numerator which gives us

$\left -(3-2x \right )$ $\displaystyle \left -(3-2x \right )$

Hence we get the following

$\frac{\left -(3-2x \right )}{3-2x}$

which is equal to $\displaystyle -1$

Report an Error

Example Question #1 : Factoring Rational Expressions

Simplify:

$\frac{x+3}{x^{2}+6x+9}$ $\displaystyle \frac{x+3}{x^{2}+6x+9}$

Possible Answers:

$\left ( x+3 \right )^{2}$ $\displaystyle \left ( x+3 \right )^{2}$

$\left ( x-3 \right )$ $\displaystyle \left ( x-3 \right )$

$\left ( x+3 \right )$ $\displaystyle \left ( x+3 \right )$

$\frac{1}{x+3}$ $\displaystyle \frac{1}{x+3}$

$\frac{1}{\left ( x+3 \right )^{2}}$ $\displaystyle \frac{1}{\left ( x+3 \right )^{2}}$

Correct answer:

$\frac{1}{x+3}$ $\displaystyle \frac{1}{x+3}$

Explanation:

If we factors the denominator we get

$\left ( x+3 \right )^{2}$ $\displaystyle \left ( x+3 \right )^{2}$

Hence the rational expression becomes equal to

$\frac{\left ( x+3 \right )}{\left ( x+3 \right )^{2}}$ $\displaystyle \frac{\left ( x+3 \right )}{\left ( x+3 \right )^{2}}$

which is equal to $\frac{1}{\left ( x+3 \right )}$ $\displaystyle \frac{1}{\left ( x+3 \right )}$

Report an Error

Example Question #303 : Variables

Which of the following fractions is NOT equivalent to $- \frac{x-5}{2x + 3}$ $\displaystyle - \frac{x-5}{2x + 3}$ ?

Possible Answers:

$\frac{\left -(x-5 \right )}{2x+3}$

$\frac{x-5}{-2x-3}$ $\displaystyle \frac{x-5}{-2x-3}$

$\frac{x-5}{\left -(2x+3 \right )}$

$\frac{x+5}{2x + 3}$ $\displaystyle \frac{x+5}{2x + 3}$

$\frac{-x+5}{2x+3}$ $\displaystyle \frac{-x+5}{2x+3}$

Correct answer:

$\frac{x+5}{2x + 3}$ $\displaystyle \frac{x+5}{2x + 3}$

Explanation:

We know that $-\frac{a}{b}$ $\displaystyle -\frac{a}{b}$ is equivalent to $\frac{-a}{b}$ $\displaystyle \frac{-a}{b}$ or $\frac{a}{-b}$ $\displaystyle \frac{a}{-b}$ .

By this property, there is no way to get $\frac{x+5}{2x+3}$ $\displaystyle \frac{x+5}{2x+3}$ from $-\frac{x-5}{2x+3}$ $\displaystyle -\frac{x-5}{2x+3}$ .

Therefore the correct answer is $\frac{x+5}{2x+3}$ $\displaystyle \frac{x+5}{2x+3}$ .

Report an Error

View Algebra Tutors

Hellen
Certified Tutor

Egerton University, Kenya, Bachelor of Education, Learning Sciences. University of Applied Sciences Nuertingen, Masters in Bu...

View Algebra Tutors

Bryan
Certified Tutor

Virginia Commonwealth University, Bachelor of Science, Mathematics and Statistics.

View Algebra Tutors

Christopher
Certified Tutor

Mansfield University of Pennsylvania, Bachelor of Science, Physics.

All Algebra 1 Resources

10 Diagnostic Tests 557 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

French Tutors in Boston, Biology Tutors in New York City, SAT Tutors in Denver, Computer Science Tutors in New York City, MCAT Tutors in Seattle, ACT Tutors in San Diego, LSAT Tutors in Phoenix, ACT Tutors in Houston, Biology Tutors in Houston, SSAT Tutors in Los Angeles

Popular Courses & Classes

MCAT Courses & Classes in Boston, MCAT Courses & Classes in Atlanta, SSAT Courses & Classes in Phoenix, GRE Courses & Classes in San Diego, MCAT Courses & Classes in Chicago, GMAT Courses & Classes in Boston, GMAT Courses & Classes in Los Angeles, ACT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Philadelphia, Spanish Courses & Classes in Chicago

Popular Test Prep

ISEE Test Prep in Denver, MCAT Test Prep in Los Angeles, MCAT Test Prep in New York City, GRE Test Prep in Philadelphia, SAT Test Prep in Denver, GMAT Test Prep in Boston, LSAT Test Prep in New York City, MCAT Test Prep in Denver, ACT Test Prep in San Francisco-Bay Area, ISEE Test Prep in Los Angeles

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra 1 : Variables

Study concepts, example questions & explanations for Algebra 1

All Algebra 1 Resources

Example Questions

Example Question #1 : How To Find The Solution To A Binomial Problem

Example Question #1 : How To Find The Solution To A Binomial Problem

Example Question #1 : How To Find The Solution To A Binomial Problem

Example Question #2 : How To Find The Solution To A Binomial Problem

Example Question #3 : How To Find The Solution To A Binomial Problem

Example Question #301 : Variables

Example Question #302 : Variables

Example Question #2 : Solving Rational Expressions

Example Question #1 : Factoring Rational Expressions

Example Question #303 : Variables

All Algebra 1 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: