Algebra II : Basic Single-Variable Algebra
Study concepts, example questions & explanations for Algebra II
All Algebra II Resources
Example Questions
Example Question #1 : Setting Up Inequalities
If 
Quadrant I
The point will land on the x or y axis, therefore there is no quadrant for the scenario.
Quadrant IV
Quadrant III
Quadrant II
Quadrant IV
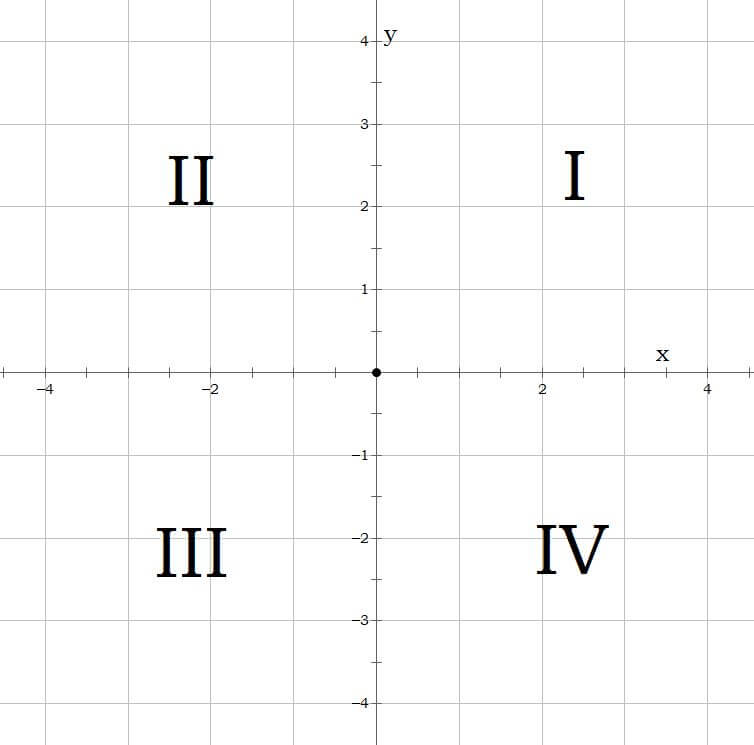
Because x is greater than zero, it will be to the right of the y axis. Because y is less than zero, it will be below the x axis. This is the fourth quadrant.
Example Question #2 : Setting Up Inequalities
At a fair, there is a game where players step on a scale and weigh themselves. The objective of the game is for the host to guess the player's weight. A player loses if the host of the game can guess the player's weight within 
For the player to lose, the host has to guess within 
Example Question #9 : Setting Up Inequalities
Set up the following inequality: Four less than three times a number squared is at least six.
Split up the inequality into parts.
A number squared:
Three times a number squared:
Four less than three times a number squared:
Is at least six:
Combine all the parts to form an inequality:
The answer is:
Example Question #1 : Setting Up Inequalities
Set up the inequality: Four times the quantity of a number less than five is more than six.
Break up the sentence into parts.
A number less than five:
The quantity of a number less than five:
Four times the quantity of a number less than five:
More than six:
Combine the terms.
The answer is:
Example Question #2041 : Algebra Ii
Set up the inequality: Four times the quantity of two less than three times a number is at most ten.
Break up the inequality into parts.
Three times a number:
Two less than three times a number:
The quantity of two less than three times a number:
Four times the quantity of two less than three times a number:
Is at most ten:
Combine the terms to form the inequality.
The answer is:
Example Question #2043 : Algebra Ii
Set up the following inequality: The product of two and the quantity of two less than five times a number must exceed twelve.
Split up the inequality into parts.
Five times a number:
Two less than five times a number:
The quantity of two less than five times a number:
The product of two and the quantity of two less than five times a number:
Must exceed twelve:
The answer is:
Example Question #201 : Basic Single Variable Algebra
Set up the inequality: Twice the quantity of three less than twice a number must be more than ten.
Break up the sentence into parts. Start with the inner quantity.
Twice a number:
Three less than twice a number:
The quantity of three less than twice a number:
Twice the quantity of three less than twice a number:
Must be more than ten:
Combine the terms to write the inequality:
The answer is:
Example Question #202 : Basic Single Variable Algebra
Set up the inequality: Four less than six times the square root of a number is at least five.
Break up the statement into parts.
The square root of a number:
Six times the square root of a number:
Four less than six times the square root of a number:
At least five:
Combine the parts to form the inequality.
The answer is:
Example Question #2045 : Algebra Ii
Set up the inequality: Five more than eight times a number must exceed fourteen.
Separate the sentence into parts and let the unknown number be 
Eight times a number:
Five more than eight times a number:
Must exceed fourteen:
Combine the parts to form the inequality.
The answer is:
Example Question #11 : Inequalities
Set up the inequality: Four less than eight times the square root of twice a number cannot be more than three.
Start with the square root.
Square root of twice a number:
Eight times the square root of twice a number:
Four less than eight times the square root of twice a number:
Cannot be more than three:
Combine the parts to form the inequality.
The answer is:
Certified Tutor
Certified Tutor
All Algebra II Resources
