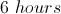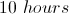Add  on both sides.

The inequality becomes:

Subtract 16 on both sides.

Divide by 10 on both sides.

Reduce both fractions.

The answer is:  

Distribute on both sides of the inequality in order to eliminate the parentheses.

The inequality becomes:

Add  on both sides.

Subtract 6 from both sides.

Divide by 17 on both sides.

The answer is:  

Add 9 on both sides.

Divide by negative three on both sides.  Dividing by a negative number will switch the sign.

The answer is:  

Multiply both sides by the least common denominator to eliminate the fractions.  The LCD is 12.

Subtract three on both sides.

Divide both sides by 8.

The answer is:  

Distribute the four through the binomial of the right side.

Add  and  on both sides.

Divide by four on both sides.

The answer is:  

Solve.

Step 1: Subtract  from both sides of the inequality.

Step 2: Subtract  from both sides of the inequality to isolate the term with the  variable.

Step 3: Multiply both sides of the inequality by -1 and reverse the inequality sign.

This is to make the inequality have only positive numbers, and this will help solve the inequality. Because we are multiplying by a negative number, we must reverse the inequality sign. The only times we reverse the inequality sign are when we are multiplying or dividing by a negative number. In other instances, we would leave the sign the same.

Step 4: Divide both sides of the inequality by .

Solution:  

Inequalities can be algebraically rearranged using operations that are mostly identical to algebraic equations, although one notable exception is multiplication or division by -1. This reverses the inequality signs. 

Multiply out by 

Subtract  from all sides, 

 Divide throughout by  and remember to reverse the inequality signs. 

It feels more natural to write  the final result as: 

Remember: Use inverse operations to undo the operations in the inequality (for example use a subtraction to undo an addition) until you are left with the variable. Make sure to do the same operations to both sides of the inequality. 

Important Note: When multiplying or dividing by a negative number, always flip the sign of an inequality.

Solution:

Expand all factors

Simplify 

Add 23

Subtract 22m

Divide by -6 (We flip the sign of the inequality)

Simplify

Start by subtracting 1 and divinding by 4 on both sides of the equality

Written in interval notation:

Tom paints for a total of  hours (2 on his own, 2 with Huck's help). Since he paints at a rate of  feet per hour, use the formula

 (or )

to determine the total length of the fence Tom paints.

 feet

Subtracting this from the total length of the fence  feet gives the length of the fence Tom will NOT paint:  feet. If Huck finishes the job, he will paint that  feet of the fence. Using , we can determine how long this will take Huck to do:

 hours.

If Huck works  hours and Tom works  hours, he works  more hours than Tom.