All Algebra II Resources
Example Questions
Example Question #1 : Fractional Exponents
Simplify the expression:
Remember that fraction exponents are the same as radicals.
A shortcut would be to express the terms as exponents and look for opportunities to cancel.
Either method, we then need to multiply to two terms.
Example Question #1 : Understanding Fractional Exponents
Convert the exponent to radical notation.
Remember that exponents in the denominator refer to the root of the term, while exponents in the numerator can be treated normally.
Example Question #1 : Fractional Exponents
Simplify:
Example Question #2 : Fractional Exponents
Write the product of 
This problem relies on the key knowledge that ![\small x^\frac{a}{b}=\sqrt[b]{x^a}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/240488/gif.latex)
Therefore, ![\small \sqrt[8]{a^{29}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/240490/gif.latex)
Example Question #3 : Fractional Exponents
Evaluate the following expression:
or
Example Question #1 : Fractional Exponents
Simplify:
Keep in mind that when you are dividing exponents with the same base, you will want to subtract the exponent found in the denominator from the exponent found in the numerator.
To find the exponent for 
To find the exponent for 
Since the exponent is negative, you will want to put the 
So then,
Example Question #4 : Fractional Exponents
Find the value of 
When you have a number or value with a fractional exponent,
or
So then,
Example Question #5 : Fractional Exponents
Find the value of
When you have a number or value with a fractional exponent,
or
So then,
Example Question #125 : Understanding Exponents
Simplify:
When exponents are raised to another exponent, you will need to multiply the exponents together.
When you have a number or value with a fractional exponent,
or
So,
Example Question #1 : Rational Exponents
Simplify:
An option to solve this is to split up the fraction. Rewrite the fractional exponent as follows:
A value to its half power is the square root of that value.
Substitute this value back into 
Certified Tutor
All Algebra II Resources





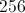

![256^{\frac{3}{4}}=\sqrt[4]{256^3}=64](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/113588/gif.latex)





![\small \small \sqrt[3]{x^7}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/39747/gif.latex)
![\small \small \sqrt[7]{x^3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/39746/gif.latex)

![x^{\frac{a}{b}}=\sqrt[b]{x^a}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/88792/gif.latex)
![x^{\frac{3}{7}}=\sqrt[7]{x^3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/110623/gif.latex)
![[x^{1/2}]^{7/3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/181666/gif.latex)





![[x^{m}]^{n}=x^{m\times n}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/27168/gif.latex)

![\small \sqrt[8]{a^2^9}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/240457/gif.latex)
![\small \sqrt[a]{8^2^9}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/240459/gif.latex)
![\small \sqrt[2]{a^5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/240461/gif.latex)
![\small \sqrt[a]{29^8}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/240460/gif.latex)
![\small \sqrt[29]{a^8}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/240458/gif.latex)
![\small a^\frac{3}{4}*a^\frac{3}{8}*a^\frac{5}{2}=a^{\frac{3}{4}+\frac{3}{8}+\frac{5}{2}}=a^{\frac{29}{8}}=\sqrt[8]{a^{29}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/240489/gif.latex)







![\bigg(\frac{27}{125}\bigg)^{\frac{1}{3}}= \sqrt[3]{\frac{27}{125}}=\frac{\sqrt[3]{27}}{\sqrt[3]{125}}=\frac{3}{5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/245056/gif.latex)












![x^{\frac{a}{b}}=\sqrt[b]{x^a}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/329507/gif.latex)
![x^{\frac{a}{b}}=(\sqrt[b]{x})^a](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/329508/gif.latex)
![9^{\frac{3}{2}}=\sqrt[2]{9^3}=\sqrt{729}=27](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/329509/gif.latex)






![x^{\frac{a}{b}}=\sqrt[b]{x^a}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/329490/gif.latex)
![x^{\frac{a}{b}}=(\sqrt[b]{x})^a](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/329491/gif.latex)
![64^{\frac{4}{3}}=\sqrt[3]{64^4}=\sqrt[3]{2^{24}}=2^8=256](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/329492/gif.latex)





![x^{\frac{a}{b}}=\sqrt[b]{x^a}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/329501/gif.latex)
![x^{\frac{a}{b}}=(\sqrt[b]{x})^a](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/329502/gif.latex)
![27^{\frac{5}{3}}=\sqrt[3]{27^5}=\sqrt[3]{3^{15}}=3^5=243](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/329503/gif.latex)














