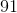All Algebra II Resources
Example Questions
Example Question #1 : How To Find The Degree Of A Polynomial
Give the degree of the polynomial.
The degree of an individual term of a polynomial is the exponent of its variable; the exponents of the terms of this polynomial are, in order, 5, 4, 2, and 7.
The degree of the polynomial is the highest degree of any of the terms; in this case, it is 7.
Example Question #1 : How To Find The Degree Of A Polynomial
What is the degree of the polynomial?
To find the degree of the polynomial, you first have to identify each term [term is for example 
EX: 

Highest degree is 
Example Question #191 : Variables
What is the degree of the polynomial?
To find the degree of the polynomial, add up the exponents of each term and select the highest sum.
12x2y3: 2 + 3 = 5
6xy4z: 1 + 4 + 1 = 6
2xz: 1 + 1 = 2
The degree is therefore 6.
Example Question #1 : Polynomial Functions
Let 



When solving functions within functions, we begin with the innermost function and work our way outwards. Therefore:
and
Example Question #2 : Polynomial Functions
Let ![\small f(x)=\sqrt[3]{x^2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/215102/gif.latex)

![\small h(x)=\sqrt[4]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/215104/gif.latex)

This problem relies on our knowledge of a radical expression ![\small \sqrt[b]{x^a}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/215106/gif.latex)

and
Example Question #1 : Polynomial Functions
Evaluate 

In problems with functions within one another, we must first solve the innermost function and then proceed outwards. Therefore, the first step is solving 
Now, we must find the values of 
Because our x term is squared in this function, both values end up being the same. Therefore, 59 is our final answer.
Example Question #2 : Polynomial Functions
Evaluate 

Beginning with the innermost function, we must first solve for 
We then take this value and plug it into 
This has no value in the real number plane, and the answer is therefore undefined.
Example Question #3 : Polynomial Functions


Determine 
Substituting -x into f(x). This has no effect on the 1st and 3rd terms. This changes the sign of the middle term.
Example Question #262 : Polynomials
Which of the following depicts a polynomial in standard form?
None of the other answers are correct.
A polynomial in standard form is written in descending order of the power. The highest power should be first, and the lowest power should be last.
The answer has the powers decreasing from four, to two, to one, to zero.
Example Question #261 : Polynomials
A polynomial consists of one or more terms where each tem has a coefficient and one or more variables raised to a whole number exponent. A term with an exponent of 0 is a constant.
Identify the expression below that is not a polynomial:
2
1
3
5
4
5
Expression 5 has the term 
All Algebra II Resources




























![\small \sqrt[3]{x^2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/215074/gif.latex)
![\small \sqrt[4]{x^3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/215075/gif.latex)
![\small \sqrt[3]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/215072/gif.latex)

![\small \sqrt[4]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/215073/gif.latex)
![\small g(h(x))=(\sqrt[4]{x})^3=x^\frac{3}{4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/215108/gif.latex)
![\small f(g(h(x)))=\sqrt[3]{(x^\frac{3}{4})^2}=\sqrt[3]{x^\frac{6}{4}}=x^\frac{6}{12}=x^\frac{1}{2}=\sqrt{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/215109/gif.latex)