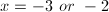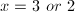Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Intermediate Single-Variable Algebra

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #111 : Factoring Polynomials

Factor the following polynomial:

$x^{2}+4x-21$

Possible Answers:

The polynomial cannot be factored

(x-7)(x-3)

(x+7)(x-3)

(x-7)(x+3)

Correct answer:

(x+7)(x-3)

Explanation:

The correct answer is . Because the constant is negative, the answer must contain terms with positive and negative constants, thus ruling out (x-7)(x-3) , which would result in a positive coefficient. The (x-7)(x+3) answer choice can be ruled out because the factored out polynomial results in a -4x , not a +4x . Therefore, the correct answer choice is, which can be confirmed if multiplied out.

Report an Error

Example Question #161 : Intermediate Single Variable Algebra

Factor 64x^2-81y^2

Possible Answers:

(8x-9y)(8x+9y)

(8x+9y)^2

Cannot be factored further.

(8x-9y)^2

Correct answer:

(8x-9y)(8x+9y)

Explanation:

This problem is an example of a difference of squares. The formula for such a problem is a^2-b^2=(a-b)(a+b) . In this problem corresponds to and corresponds to . Therefore, the solution is (8x-9y)(8x+9y) .

Report an Error

Example Question #161 : Intermediate Single Variable Algebra

Simplify $\frac{(7x-4)}{(4-7x)}$

Possible Answers:

None of the other answers

Answer cannot be simplified further.

Correct answer:

Explanation:

When working with problems like these, you want to put the monomials in a standard format with the highest ordered terms on the left.

So the denominator should read: -7x+4

The entire expression will then read: $\frac{(7x-4)}{(-7x+4)}$

Then factor out a from the equation so it reads $-1\times(\frac{(-7x+4)}{(-7x+4)})$

The like terms then cancel leaving .

Report an Error

Example Question #1 : Simplifying And Expanding Quadratics

Solve the equation for .

$\small \frac{1}{x}=\frac{x+1}{6}$

Possible Answers:

$\small x=-3\ or\ 2$

$\small x=3\ or\ -2$

$\small x=-3\ or\ -2$

$\small x=3\ or\ 2$

Correct answer:

$\small x=-3\ or\ 2$

Explanation:

$\small \small \frac{1}{x}=\frac{x+1}{6}$

Cross multiply.

$\small 6=x(x+1)$

$\small 6=x^2+x$

Set the equation equal to zero.

$\small 0=x^2+x-6$

Factor to find the roots of the polynomial.

3*-2=-6 and 3+(-2)=1

$\small 0=(x+3)(x-2)$

$\small 0=x+3; x=-3$

$\small 0=x-2; x=2$

Report an Error

Example Question #2 : Simplifying And Expanding Quadratics

$Expand \; (5x^2 +x + 1)(3x-2)$

Possible Answers:

15 x^2-6 x-2

8x^3-7 x^2+x-2

15 x^3+7 x^2-x-2

15 x^3-7 x^2+x-2

Correct answer:

15 x^3-7 x^2+x-2

Explanation:

$Multiply \; (3 x-2) (5 x^2+x+1)\; using \; a \; grid$

$Answer: \; 15 x^3-7 x^2+x-2$

Report an Error

Example Question #3 : Simplifying And Expanding Quadratics

Solve the equation for :

$\frac{x}{2}=\frac{-1}{x+3}$

Possible Answers:

x=-1, x=-2

x=0

x=1, x=0

x=1

x=1, x=2

Correct answer:

x=-1, x=-2

Explanation:

$\frac{x}{2}=\frac{-1}{x+3}$

1. Cross multiply:

$x^{2}+3x=-2$

2. Set the equation equal to :

$x^{2}+3x+2=0$

3. Factor to find the roots:

(x+2)(x+1)=0

x+2=0 , so x=-2

x+1=0 , so x=-1

Report an Error

Example Question #2 : Quadratic Equations And Inequalities

If you were to solve $x^{2}+8x+9=0$ by completing the square, which of the following equations in the form (x+f)^2=g do you get as a result?

Possible Answers:

(x+8)^2=64

(x+8)^2=16

(x+4)^2=7

(x+4)^2=16

(x+4)^2=25

Correct answer:

(x+4)^2=7

Explanation:

When given a quadratic in the form x^2+bx+c=0 and told to solve by completing the square, we start by subtracting from both sides. In this problem is equal to , so we start by subtracting from both sides:

x^2+8x=-9

To complete the square we want to add a number to each side which yields a polynomial on the left side of the equals sign that can be simplified into a squared binomial (x+d)^2 . This number is equal to $(\frac{b}{2})^2$ . In this problem is equal to , so:

$(\frac{b}{2})^2=(\frac{8}{2})^2=4^2=16$

We add to both sides of the equation:

x^2+8x+16=-9+16

We then factor the left side of the equation into binomial squared form and combine like terms on the right:

(x+4)^2=7

Report an Error

Example Question #4 : Simplifying And Expanding Quadratics

If you were to solve $x^{2}+4x-5=0$ by completing the square, which of the following equations in the form (x+f)^2=g do you get as a result?

Possible Answers:

(x+2)^2=5

(x+2)^2=7

(x+2)^2=9

(x+2)^2=21

(x-2)^2=9

Correct answer:

(x+2)^2=9

Explanation:

x^2+4x=5

To complete the square we want to add a number to each side which yields a polynomial on the left side of the equation that can be simplified into a squared binomial (x+d)^2 . This number is equal to $(\frac{b}{2})^2$ . In this problem is equal to , so:

$(\frac{b}{2})^2=(\frac{4}{2})^2=2^2=4$

We add to both sides of the equation:

x^2+4x+4=5+4

We then factor the left side of the equation into binomial squared form and combine like terms on the right:

(x+2)^2=9

Report an Error

Example Question #1 : Simplifying And Expanding Quadratics

Expand:

(4x-1)(-2x+3)

Possible Answers:

$-8x^{2}+14x-3$

$8x^{2}+10x-3$

$8x^{2}+14x-3$

$-8x^{2}+10x-3$

None of the other answers are correct.

Correct answer:

$-8x^{2}+14x-3$

Explanation:

Use the FOIL method, which stands for First, Inner, Outer, Last:

(4x)(-2x)+(4x)(3)+(-1)(-2x)+(-1)(3)

= -8x^2+12x+2x-3

$=-8x^{2}+14x-3$

Report an Error

Example Question #3 : How To Multiply Polynomials

Multiply: $(x^{2} + 3) (4x - 1)$

Possible Answers:

$4x^{3} - 3$

$4x^{3} -x^{2} -12x + 3$

$4x^{3} +x^{2} -12x - 3$

$4x^{3} + 3$

$4x^{3} -x^{2} +12x - 3$

Correct answer:

$4x^{3} -x^{2} +12x - 3$

Explanation:

$(x^{2} + 3) (4x - 1)$

$= x^{2} (4x - 1) + 3(4x - 1)$

$= x^{2} \cdot 4x - x^{2} \cdot 1 + 3 \cdot 4x - 3 \cdot 1$

$= 4x^{3} - x^{2} + 12x - 3$

Report an Error

View Algebra 2 Tutors

Robert
Certified Tutor

University of Pittsburgh, Bachelor of Science, Physics.

View Algebra 2 Tutors

Eric
Certified Tutor

University of Wisconsin-Madison, Bachelor of Science, Applied Physics.

View Algebra 2 Tutors

Samuel
Certified Tutor

Millikin University, Bachelor of Science, Mathematics.

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Boston, ACT Tutors in Denver, LSAT Tutors in San Francisco-Bay Area, Computer Science Tutors in New York City, GRE Tutors in Seattle, MCAT Tutors in Seattle, Physics Tutors in San Diego, Spanish Tutors in Seattle, GRE Tutors in Atlanta, SAT Tutors in Atlanta

Popular Courses & Classes

MCAT Courses & Classes in Miami, ACT Courses & Classes in Los Angeles, ACT Courses & Classes in Washington DC, SSAT Courses & Classes in New York City, ISEE Courses & Classes in Chicago, SAT Courses & Classes in Dallas Fort Worth, ACT Courses & Classes in San Diego, LSAT Courses & Classes in Houston, MCAT Courses & Classes in Houston, SAT Courses & Classes in Chicago

Popular Test Prep

SAT Test Prep in Washington DC, SSAT Test Prep in Dallas Fort Worth, SSAT Test Prep in Houston, SSAT Test Prep in Washington DC, GRE Test Prep in Dallas Fort Worth, MCAT Test Prep in Chicago, ACT Test Prep in Washington DC, ISEE Test Prep in Miami, MCAT Test Prep in Boston, ISEE Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Intermediate Single-Variable Algebra

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #111 : Factoring Polynomials

Example Question #161 : Intermediate Single Variable Algebra

Example Question #161 : Intermediate Single Variable Algebra

Example Question #1 : Simplifying And Expanding Quadratics

Example Question #2 : Simplifying And Expanding Quadratics

Example Question #3 : Simplifying And Expanding Quadratics

Example Question #2 : Quadratic Equations And Inequalities

Example Question #4 : Simplifying And Expanding Quadratics

Example Question #1 : Simplifying And Expanding Quadratics

Example Question #3 : How To Multiply Polynomials

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: