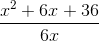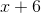All Algebra II Resources
Example Questions
Example Question #90 : Rational Expressions
Add:
Evaluate by changing the denominator of the second fraction so that both fractions have similar denominators.
Use distribution to simplify the numerator.
Combine like-terms.
The answer is:
Example Question #91 : Rational Expressions
Add:
In order to subtract the fractions, we will need to determine the least common denominator.
Multiply the second fraction's numerator and denominator by ten, since both fractions share an x-term.
Combine the numerator to form one fraction.
The answer is:
Example Question #92 : Rational Expressions
Solve:
In order to add the numerators, we will need to find the least common denominator.
Use the FOIL method to multiply the two denominators together.
Simplify by combining like-terms. The LCD is:
Change the fractions.
Simplify the fractions.
Combine like-terms.
The answer is:
Example Question #93 : Rational Expressions
Add:
Determine the least common denominator in order to add the numerator.
Each denominator shares an 

Convert the fractions.
Simplify the top and bottom.
The answer is:
Example Question #94 : Rational Expressions
Solve:
Determine the least common denominator. Each term will need an x-variable, and all three denominators will need a common coefficient.
The least common denominator is 
Convert the fractions.
The expression becomes:
The answer is:
Example Question #95 : Rational Expressions
Subtract:
Notice that 

Convert the fractions.
Simplify the fractions and combine as one fraction.
The expression becomes:
Combine like-terms.
Factor out a negative one from the numerator to pull the negative sign in front of the fraction.
The answer is:
Example Question #96 : Rational Expressions
For all positive values of x, which of the following expressions is equivalent to the following:
In order to add the numerators in this expression, we will need to calculate the least common denominator. In this case, the least common denominator is 
Now convert the right fraction to a form with the same denominator. Again, multiply the fraction by a value of one in the following form:
Now, we can add our two fractions by rewriting them as one whole fraction.
Simplify the numerator.
This cannot be reduced or simplified any further; therefore, the answer is:
Example Question #1 : Multiplying And Dividing Rational Expressions
What is the slant asymptote of 
To find the slant asymptote, we have to divide the numerator by the denominator and see the equation of the line that we get.
Our long division problem ends up looking like this:
(We can ignore the remainder because it doesn't sufficiently impact the equation of the asymptote, especially as 
Thus, the equation of the slant asymptote is 
Example Question #1 : Multiplying And Dividing Rational Expressions
Which is a simplified form of 
Example Question #2 : Multiplying And Dividing Rational Expressions
Simplify the following expression:
Our first step in this problem would be to distribute the exponent on the second term, which makes the expression become:
We then multiply like terms, remembering that multiplying like terms with exponents means we will add the exponent, so the expression becomes:
Certified Tutor
All Algebra II Resources







}{[9]x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/837832/gif.latex)
}{[9]x} =\frac{7}{9x}+\frac{72-18x}{9x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/837833/gif.latex)