All AP Chemistry Resources
Example Questions
Example Question #41 : Gases
If a container holds 1mol of hydrogen, 2.5mol of helium, and 2mol of oxygen at a total pressure of 4atm, what is the partial pressure of the oxygen gas?
According to Dalton's law of partial pressures, when two or more gases are in one container without chemical interaction, each behaves independently of the others. The partial pressure of oxygen can, therefore, be found by multiplying the molar fraction of oxygen in the container by the total pressure of the three gases.
Example Question #151 : Solutions And States Of Matter
A glass container holds a mixture of two gases. Gas A exerts a pressure of 5atm on the container.
If there are twice as many moles of gas A as there are moles of gas B in the container, what is the total pressure in the container?
The pressure is unaffected by the gas of lower concentration
This is an equation which requires us to find the partial pressures of each gas in the container. The equation for partial pressure is 

Example Question #45 : Gases
A gas mixture at equilibrium held over water at 

The molar quantity of a gas is directly proportional to its partial pressure, so if we have a total of 12 moles of gas, and 

Example Question #1 : Balancing Chemical Equations
What is the formula for the dissociation of iron (II) phosphate?
Iron (II) has a positive two charge: 
Phosphate has a negative three charge: 
The initial compound must be constructed to cancel these charges. The dissociation is: 
Example Question #1 : Solubility
Pb(OH)2 has a Ksp of 1.43 * 10-20.
What is its solubility?
1.53 * 10-7M
2.43 * 10-7M
1.20 * 10-10M
8.42 * 10-12M
1.53 * 10-7M
Lead (II) hydroxide dissociates according to this reaction: 
Ksp = [Pb2+][OH-]2
If [Pb2+] = x, then [OH-] = 2x. They exist in a 1:2 ratio.
Ksp = 1.43 * 10-20 = x(2x)2 = 4x3
x = 1.53 x 10-7M
Example Question #2 : Solubility
Which of the following factors will generally lead a solute to dissolve more easily into a solution (i.e. increase solubility)?
Increasing the temperature of the solution
None of these choices will increase solubility
Decreasing the temperature of the solution
The common ion effect
Increasing the temperature of the solution
Increasing the temperature of a solution will generally increase its solubility, while decreasing temperature will have the opposite effect. The common ion effect refers to the phenomenon when two compunds in a solution dissociate to produce at least one similar ion, and will make it harder for additional amounts of that ion in the solution to dissociate, decreasing solubility.
Example Question #3 : Solubility
If the Ksp of the above dissociation is found to be 2.70 * 10-4, what is the solubility of NaCl?
7.29 * 10-8M
1.44 * 10-2M
1.89 * 10-2M
1.64 * 10-2M
1.64 * 10-2M
First, set up a balanced reaction and enter X for the amount of each solute that is going to be dissolved. As NaCl dissociates, each ion amount will increase by some amount, X.




Then set up the equation for the value of Ksp and enter in the value of X for each solute. Use this equation to solve for X, the solubility (in mol/L). Remember that NaCl si not included in the equation, as it is a pure solid.
Example Question #1 : Solubility
If the solubility of CaF2 in the dissociation reaction above was determined to be 1.54 * 10-3M, what is the Ksp value for CaF2?
1.98 * 10-8
1.46 * 10-8
1.42 * 10-6
2.24 * 10-6
1.46 * 10-8
Use the balanced reaction of the dissociation to assign values of X for the solubility of each ion. As CaF2 dissociates, each ion amount will increase by some amount; calcium will increase by X and flouride will increase by 2X.




Then plug in the equation to solve Ksp, using the X values assigned for each solute. Use the given value for solubility to find Ksp. Remember that NaCl si not included in the equation, as it is a pure solid.
Example Question #1 : Solubility
Consider the following balanced equation for the solubility of barium hydroxide in an aqueous solution.
What is the solubility of barium hydroxide?
In order to solve for the solubility of barium hydroxide, we need to establish an ICE table for the reaction.
I. Initially, there are no barium ions or hydroxide ions in the solution, so we can call their concentrations zero at the beginning of the reaction.
C. For every molecule of dissolved barium hydroxide, there will be one ion of barium and two ions of hydroxide. As a result, the increases in each ion can be designated 

E. Finally, we plug these values into the equilibrium expression and set it equal to the solubility product constant.
Example Question #6 : Solubility
Four different insoluble salts are added to an aqueous solution in equal amounts. Assume that the salts do not interact with one another in any way. The following list shows the salts and their solubility product constants.



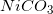
Which of the following ions will have the highest concentration in the solution?
The solubility product constants help us envision which ions will have the largest concentrations after dissolving to equilibrium. 
Upon the dissolving of 

Certified Tutor
All AP Chemistry Resources































![K_{sp}= [Na^{+}][Cl^{-}] = (X)(X) = X^{2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/85510/gif.latex)






![K_{sp}= [Ca^{2+}][F^-]^2=(X)(2X)^{2} = 4X^{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/119041/gif.latex)








![K_{sp}=[Ba^{2+}][OH^-]^2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/94058/gif.latex)
![\small 5*10^{-3} = [x][2x]^{2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/126927/gif.latex)






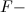



![[F^-]<[CrO_4^{2-}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/119420/gif.latex)



