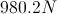We can use the equation for conservation of energy to solve this problem:

Plugging in our expressions and canceling initial kinetic and final potential energy, we get:

Rearranging for the coeffeicient of friction:

We now need to determine expressions for the normal force and the distance the sledder travels:

Normal force:

Distance of slope:

Plugging these into the expression for the coefficient of friction, we get:

We know all of our variables, allowing us to solve:

Work is equal to the change in energy of the system. We are given the weight of the box and the vertical displacement, which will allow us to calculate the change in potential energy. This will be the total work required to move the box against gravity.

The remaining work that the man exerts must have been used to counter the force of friction acting against his motion.

Now we know the work performed by friction. Using this value, we can work to solve for the force of friction and the coefficient of friction. First, we will need to use a second formula for work:

In this case, the distance will be the distance traveled along the surface of the incline. We can solve for this distance using trigonometry.

We know the work done by friction and the distance traveled along the incline, allowing us to solve for the force of friction.

Finally, use the formula for frictional force to solve for the coefficient of friction. Keep in mind that the force on the box due to gravity will be equal to .

Plug in our final values and solve for the coefficient of friction.

In order for the crate to not slide, the truck has to exert a frictional force on it. The force of friction is related to the normal force by the coefficient of friction.

This frictional force comes from the acceleration of the truck, based on Newton's second law.

The two forces will be equal when the truck is at maximum acceleration without the crate moving.

Solve for the acceleration.

We can use the equation for conservation of energy to solve this problem.

The work in this scenario is done by friction. The only term we can remove from this equaiton is final potential energy. Substituting expressions for each term, we get:

We need to determine initial height and the normal force of the skier before we can solve for the coefficient of friction.

Substitute these into the original equation:

Canceling out mass and rearranging for the coefficient of friction, we get:

Plug in our given values to solve:

The maximum force that can be applied will be equal to the maximum value of the static friction force. The formula for friction is:

We also know that the normal force is equal and opposite the force of gravity.

Substituting to the original equation, we can rewrite the force of friction.

Using the given values for the coefficient of friction and mass, we can calculate the force using the acceleration of gravity.

We first draw a force diagram:

Note that since the box is originally moving with a velocity of , it is moving to the right since its velocity is positive. This implies that friction, which always opposes motion, is directed to the left as shown in the diagram. From our diagram we have the following equations:

 and 

To know how much time it will take for the box to stop, we need to know the acceleration of the box. Note that the acceleration is constant since friction is a constant force acting on the box. We can fin friction using the following equation:

, where  is the coefficient of friction and  the normal force. So we have;

Now that we know our acceleration, we can figure out how much time it will take the box to come to a box with the following equation:

Where the final velocity is  since the box comes to a stop.

Note that there is no such thing as negative time, so you should be able to dismiss those answer choices right away. You must be very careful with using the correct signs for every vector.

Recall the formula to determine kinetic friction:

Here,  is the kinetic friction force,  is the constant of friction, and  is the magnitude of the normal force of the object in question. Recall that the formula for the normal force is given by:

Here,  is the mass of the object,  is the gravitational constant, and  is the angle of elevation. Since the object is lying  to the horizontal, the normal force it feels is:

Therefore,

To solve for the units, we simply have to solve for  and determine its units. 

Both friction and normal forces have units of newtons , which means that  has units . 

Therefore,  is a dimensionless term and has no units. 

The equation for frictional force is given by:

Because the crate is on a horizontal platform, the normal force is equal to the weight force . Multiply the normal force by the given coefficient of kinetic friction  and solve for the frictional force:

Note that the coefficient of friction is unitless because it is a ratio and therefore our answer comes out in Newtons. Also note that the force of friction is in a direction that opposes motion.

We can use one of the kinematic equations to our advantage: 

We are given the player's speed and the distance the player slide into home plate. What is implied is that the player's final velocity . We can also rewrite the acceleration  in terms of the player's mass and the forces acting on him (which is only friction)

Substitute this into the kinematic equation and solve for the coefficient of kinetic friction,