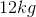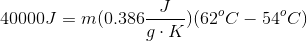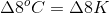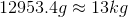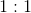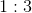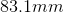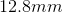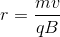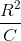All AP Physics B Resources
Example Questions
Example Question #1 : Understanding Heat And Temperature
Which of the following is not an acceptable unit for specific heat?
Specific heat is most commonly applied in the equation to determine the heat required/released during a temperature change:
Rearranging this equal, we can see that this units of specific heat are units of heat per units of mass times units of temperature.
Heat energy can have the units of Joules or calories. Mass can have units of grams or kilograms. Temperature can have units of Kelvin, degrees Celsius, or degrees Fahrenheit. British thermal units (Btu) is a less common unit of heat, defined by the amount of heat required to raise one pound of water by one degree Fahrenheit.
Newtons are a unit of force, and cannot be used in the units for specific heat.
Example Question #1 : Understanding Heat And Temperature
A sample of copper is heated with 


Our equation for temperature change using specific heat is:
Since Celsius and Kelvin use the same interval scale, we do not need to convert to find the change in temperature. Using the initial and final temperatures, the energy input, and the specific heat of copper, we can calculate the mass of copper present.
To simplify, we will solve for the temperature change separately.
Since the scale for Celsius and Kelvin is the same, this change is the same in either scale.
Use this value back in the original calculation.
Convert to kilograms to simplify.
Example Question #1 : Thermodynamics And Heat




Since the ice melts, this action occurs in three stages.
1) The heating of the ice to its melting point
2) The melting of the ice into water
3) The heating of the water after it is melted
When a temperature change is involved, the relationship of heat input to temperature change is given by:
In this formula, 
So this situation is encompassed by three expressions, representing the three parts of the problem, each of which deals with the same mass of material, 


1)
2) 
3) 
The values for 



Using this equation we can solve for the final temperature.
Example Question #1 : Electricity
Charges A and B are placed a distance of 




A student places these two charges in a vacuum medium and measures 

The dielectric constant of glass is 
You can simplify this question tremendously by using the definition of a dielectric constant. Dielectric constant is defined as the ratio of the electrostatic force in vacuum to the electrostatic force in the medium (in this case glass).
The question is asking for the reciprocal of this value: the ratio of the force in glass to the force in the vacuum. Our answer is calculated by taking the reciprocal of the dielectric constant of glass.
Example Question #1 : Ap Physics 2
How much work is done by the electric field moving an electron along an equipotential surface with a potential of 
We must know the strength of the electric field to solve
Moving a charge along an equipotential surface will involve no work done by the electric field. The potential is constant throughout an equipotential surface; therefore, the potential difference experienced by the electron will be zero. Remember that energy is dependent on the potential difference.
If the potential difference is zero then the energy (and work) will be zero.
Example Question #71 : Ap Physics B
Charges A and B are placed a distance of 




What is the ratio of 

This question is very simple if you realize that the force experienced by both charges is equal.
The definition of the two electrostatic forces are given by Coulomb's law:
In this question, we can rewrite this equation in terms of our given system.
It doesn’t matter if the charges of the two particles are different; both particles experience the same force because the charges of both particles are accounted for in the electrostatic force equation (Coulomb's law). This conclusion can also be made by considering Newton's third law: the force of the first particle on the second will be equal and opposite the force of the second particle on the first.
Since the forces are equal, their ratio will be 
Example Question #1 : Coulomb's Law
An excess charge of 



Two principal realizations help with solving this problem, both derived from Gauss’ law for electricity:
1) The excess charge on an ideal conducting sphere is uniformly distributed over its surface
2) A uniform shell of charge acts, in terms of electric force, as if all the charge were contained in a point charge at the sphere’s center
With these realizations, an application of Coulomb’s law answers the question. If 

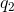
In this equation, 



Using the given values in this equation, we can calculate the generated force:
Example Question #2 : Magnetic Force
A proton traveling at 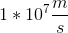


The proton’s mass is 


A charged particle moving through a perpendicular magnetic field feels a Lorentz force equal to the formula:



We can set these two equations equal to one another, allowing us to solve for the radius of the arc.
Once the particle travels through a semicircle, it is laterally one diameter in distance from where is started (i.e. twice the radius of the circle).
Twice this value is the lateral offset of its crash point from the entrance:
Example Question #1 : Electricity And Magnetism
An ideal transformer, under a purely resistive load, consists of an iron core that directs all the magnetic flux from a primary winding through a secondary winding. The primary winding has 


In basic consideration, the electrical transformer works directly according to Faraday’s law, following the picture given below.

If the coils are wound tightly enough that the magnetic flux generated in any of them effectively passes undiminished through all of them, and the iron core directs all the magnetic flux from the primary to secondary coil with insignificant losses, then Faraday’s law points a direct path from 

If there are 

From the figure, it is seen that the voltages in each line are dropped over all loops together. Hence, for the primary winding, by Faraday’s law:
For the secondary winding:
Here, 


This can be used to solve the problem above:
NOTE: This only works under alternating current. Otherwise, there is no change in current to create the changing magnetic flux on which the transformer depends.
Example Question #71 : Ap Physics B
Which of the following is equal to the time constant of an RC circuit?
The definition of a time constant for an RC circuit is the product of resistance and charge:
This is defined as the time it takes the capacitor to reach a charge that is around 63% of the maximum charge. It is also the time it takes to discharge around 37% of the charge. This value is commonly used to determine the amount of charge a capacitor has or the amount of current flowing through the capacitor at any given time point.
All AP Physics B Resources