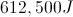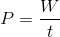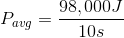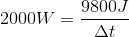All AP Physics B Resources
Example Questions
Example Question #21 : Ap Physics 1
A 


First, we calculate the initial kinetic energy of the car:
Then, calculate the final kinetic energy after the car has reached a velocity of 
To find the change in kinetic energy, we subtract the initial energy from the final energy.
This answer in positive because the car gains energy when it increases its velocity.
Example Question #1 : Understanding Kinetic Energy
A 

The first thing we need to find is the final velocity of the car. We know it starts from rest and has an acceleration of 
The formula for kinetic energy is:
We can use the calculated final velocity and the mass of the car to determine its final kinetic energy.
Example Question #61 : Newtonian Mechanics
A uniform thin hoop of mass 


Note that the moment of inertia of a uniform thin hoop of mass 


The total kinetic energy for an object rolling without slipping is the sum of its translational and rotational kinetic energies.
The translational kinetic energy treats the object as if it were a mass sliding along at a constant velocity. We can calculate the translational kinetic energy using the equation:
Use this equation with the given mass and velocity to solve for translational kinetic energy.
The rotational kinetic energy is given by the formula:
In this equation, 

The relationship between angular and linear velocity in the case of a hoop rolling without slipping is:
Solve for the moment of inertia and the angular velocity of the hoop.
Use these values in the formula for rotational kinetic energy.
The total kinetic energy is the sum of the translational and rotational kinetic energies.
Example Question #61 : Ap Physics B
A crane lifts a 

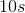
To find average power, we find the total work done by the crane in lifting the steel beam, and then divide it by the time taken to complete the task.
In this case, the total work done is equal to the change in potential energy of the steel beam. for this, we use the potential energy equation:
We then divide the work by 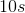
Example Question #11 : Work, Energy, And Power
A crane is being used to lift a 


First we find the total work required to lift the crate:
We are given the mass, change in height, and the acceleration of gravity. Using these values, we can solve for the total work done.
Next, we can use the equation for power to find the time to complete this task if the engine is working at its maximum power.
Certified Tutor
Certified Tutor
All AP Physics B Resources