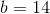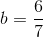First, add 6 to both sides so that the term with "x" is on its own.

$\displaystyle 2x=20$

Now, divide both sides by 2.

$\displaystyle x=10$

Start by isolating the term with $\displaystyle b$ to one side. Add 10 on both sides.

$\displaystyle 7b=14$

Divide both sides by 7.

$\displaystyle b=2$

First start by distributing the 7.

$\displaystyle 7(t-2)=7t-14$

$\displaystyle 7t-14=21$

Now, add both sides by 14.

$\displaystyle 7t=35$

Finally, divide both sides by 7.

$\displaystyle t=5$

Start by adding 10 to both sides of the equation.

$\displaystyle 9g=81$

Then, divide both sides by $\displaystyle 9$.

$\displaystyle g=9$

First, add $\displaystyle 7$ to both sides of the equation:

$\displaystyle 3x=21$

Then, divide both sides by $\displaystyle 3$:

$\displaystyle x=7$

When solving an equation, we need to find a value of x which makes each side equal each other. We need to remember that $\displaystyle \small 6x+9$ is equal to and the same as $\displaystyle \small 45$. When we solve an equation, if we make a change on one side, we therefore need to make the exact same change on the other side, so that the equation stays equal and true. To illustrate, let's take a numerical equation:

$\displaystyle \small \small 2\times3+4=10$

If we subtract $\displaystyle \small 4$ from each side, the equation still remains equal:

$\displaystyle \small 2\times3+4-4=10-4$

$\displaystyle \small 2\times3=6$

If we now divide each side by $\displaystyle \small 3$, the equation still remains equal:

$\displaystyle \small \frac{2\times3}{3}=\frac{6}{3}$

$\displaystyle \small 2=2$

This still holds true even if we have variables in our equation. We can perform the inverse operations to isolate the variable on one side and find out what number it's equal to. To solve our problem then, we need to isolate our $\displaystyle \small x$ term. We can do that by subtracting $\displaystyle \small \small 9$ from each side, the inverse operation of adding $\displaystyle \small \small 9$:

$\displaystyle \small 6x+9-9=45-9$

$\displaystyle \small 6x=36$

We now want there to be one $\displaystyle \small x$ on the left side. $\displaystyle \small 6x$ is the same thing as $\displaystyle \small 6\times x$, so we can get rid of the 6 by performing the inverse operation on both sides, i.e. dividing each side by $\displaystyle \small 6$:

$\displaystyle \small \frac{6x}{6}=\frac{36}{6}$

$\displaystyle \small x=6$ is therefore our final answer.

The answer is $\displaystyle x=23$. The goal is to isolate the variable, $\displaystyle x$, on one side of the equation sign and have all numerical values on the other side of the equation.

Since $\displaystyle -418$ is a negative number, you must add $\displaystyle 418$ to both sides.

$\displaystyle 20x = 460$

Then, divide both sides of the equation by $\displaystyle 20$:

$\displaystyle x=\frac{460}{20} = 23$