All Basic Geometry Resources
Example Questions
Example Question #1 : How To Find An Angle In A Right Triangle
Find angle C.
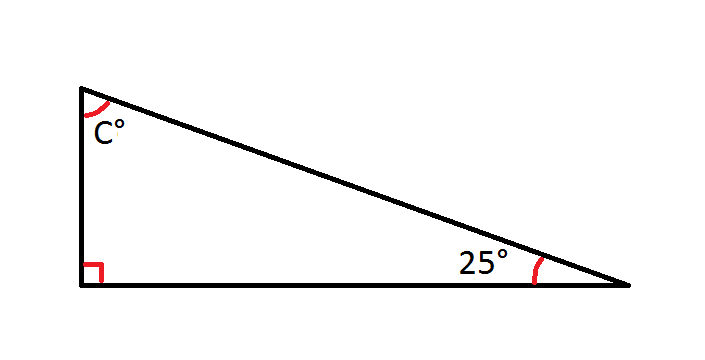
None of these
C=65
C=70
C=53
C=72
C=65
First, know that all the angles in a triangle add up to 180 degrees.
Each triangle has 3 angles. Thus, we have the sum of three angles as shown:
where we have angles A, B, and C. In our right triangle, one angle is 25 degree and we'll call that angle A. The other known angle is 90 degrees and we'll call this angle B. Thus, we have
Simplify and solve for C.
Example Question #321 : Right Triangles
Which of the following can be two angle measures of a right triangle?
A right triangle cannot have an obtuse angle; this eliminates the choice of 100 and 10.
The acute angles of a right triangle must total 90 degrees. Three choices can be eliminated by this criterion:
The remaining choice is correct:
Example Question #1 : How To Find An Angle In A Right Triangle
A right triangle has an angle that is 15 more than twice the other. What is the smaller angle?
The sum of the angles in a triangle is 180. A right triangle has one angle of 90. Thus, the sum of the other two angles will be 90.
Let 

So the equation to solve becomes 
Thus, the first angle is 

So the smaller angle is
Example Question #1 : How To Find An Angle In A Right Triangle
Angle 






The interior angles of a triangle always add up to 180 degrees. We are given angle 

Angle 
Example Question #3 : How To Find An Angle In A Right Triangle
Which of the following cannot be true of a right triangle?
One leg can be longer than the hypotenuse.
A right triangle can be equilateral.
None of the other statements can be true of a right triangle.
A right triangle can have an obtuse angle.
The measures of the angles of a right triangle can total 
None of the other statements can be true of a right triangle.
All of these statements are false.
A right triangle can be equilateral.
False: An equilateral triangle must have three angles that measure 
One leg can be longer than the hypotenuse.
False: Each leg is shorter than the hypotenuse.
A right triangle can have an obtuse angle.
False: Both angles of a right triangle that are not right must be acute.
The measures of the angles of a right triangle can total 
False: The measures of any triangle total 
Example Question #321 : Right Triangles
The formula to find all the angles of a triangle is:


To solve for the measure of angle 






Example Question #1 : How To Find An Angle In A Right Triangle
Find the degree measure of the missing angle.
All the angles in a triangle add up to 180º.
To find the value of the remaining angle, subtract the known angles from 180º:
Therefore, the third angle measures 43º.
Example Question #1 : How To Find An Angle In A Right Triangle
The right triangle 
The internal angles of a triangle always add up to 180 degrees, and it was given that the triangle was right, meaning that one of the angles measures 90 degrees.
This leaves 90 degrees to split evenly between the two remaining angles as was shown in the question.
Therefore, each of the two equal angles has a measure of 45 degrees.
Example Question #2 : How To Find An Angle In A Right Triangle
What is the missing angle in this right triangle?
The angles of a triangle all add up to 
This means that 
Using the fact that 90 is half of 180, we can figure out that the missing angle, x, plus 34 adds to the remaining 90, and we can just subtract

Example Question #3 : How To Find An Angle In A Right Triangle
Solve for 
The angles of a triangle add together to 180 degrees. We already know that one of the angles is 90 degrees, so we can subtract 90 from 180: the other 2 angles have to add to 90 degrees.
We can now subtract to get x:
All Basic Geometry Resources






















 , what is the measure of angle
, what is the measure of angle  ?
?