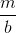To solve this problem, we can use either the quotient rule or the product rule.  For this solution, we will use the product rule.  

The product rule states that .  

In this case, let  and .  

Putting both of these together, we get 

.

To find the slope of the tangent line at the specified point, we must first verify that the specified point actually exists on the curve. We check that 

Since the verification checks out, the problem has a solution and we can continue with Implicit Differentiation. 

Recall that for Implicit differentiation, if we have a function in terms of y, we have that it's derivative with respect to x is 

Applying this to the given function, we have that 

We must also utilize the Chain Rule to obtain the derivative; we get that

Algebraically, we divide the cosine term to begin isolating dy/dx. We then get that

To obtain the slope of the tangent line, we substitute the specified point (x,y) for x and y respectively. 

The volume of a sphere is 

which can also be written as a function with respect to time, i.e.. 

.  

If we take the derivative of this, then 

.  

The problem tells us though that the rate of change of the radius is  and .  

Plugging in these values we find that 

.

To do a linear approximation, we're going to create a function

, that approximates our situation. In our case, m will be the slope of the function  at , while b will be the value of the function  at . The z will be distance from our starting position  to our end position , which is . 

Firstly, we need to find the derivative of  with respect to x to determine slope.

By the power rule: 

The slope at  will therefore be 0 since .

Since this is the case, the approximate value of our interest rate will be identical to the value of the original function at x=2, which is . 

1 is our final answer. 

To do this, we must determine the slope of the function at , which we will call , and the initial value of the function at , which we will call , and since  is only  away from , our linear approximation will look like:

To determine slope, we take the derivative of the function with respect to x and find its value at , which in our case is:

At , our value for  is 

To determine , we need to determine the value of the original equation at 

At , our value for b is  

Since , 

First recall that

To find the tangent line of  at , we first determine the slope of . To do so, we must find its derivative. 

Recall that derivatives of exponential functions involving  are given as:

, where  is a constant and  is any function of 

In our case, ,. 

At ,

 , where  is the slope of the tangent line.

To use point-slope form, we need to know the value of the original function at , 

Therefore,

At , 

The population size  after some time  is given by:

where  is the initial population.

At the start, there were 30 blood cells.

Substitute this value into the given formula.

After 2 hours, 45 blood cells were present.  Write this in mathematical form.

Substitute this into , and solve for .

Direct constant of proportionality for any given function y, between any x values, is given by

, where  is the direction constant of proportionality

In the case of a linear function 

 is the same thing as the slope. 

Therefore, the constant of proportionality is 

To determine the direct constant of proportionality, we determine the rate of change from  and  for .

Rate of change is determined by

.

In our case,  between  and , the rate of change is

.

Direct constant of proportionality  is given by

.

Since  and