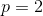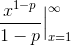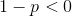Call Now to Set Up Tutoring:

(888) 888-0446

Calculus 2 : Comparing Series

Study concepts, example questions & explanations for Calculus 2

Create An Account

All Calculus 2 Resources

9 Diagnostic Tests 308 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #161 : Series In Calculus

We consider the following series:

$\sum_{n=0}^{\infty} \frac{n}{n^2+1}$$

Determine the nature of the convergence of the series.

Possible Answers:

$\frac{1}{2}$

The series is divergent.

$\frac{3}4{}$

Correct answer:

The series is divergent.

Explanation:

We will use the Comparison Test to prove this result. We must note the following:

$\frac{n}{n^2+1}$ is positive.

We have all natural numbers n:

$n^2\ge n$ , this implies that

$n^2+1\ge n+1 > n$ .

Inverting we get :

$\frac{1}{n} <\frac{n}{n^2+1}$

Summing from 1 to $\infty$ , we have

$\sum_{n=1}^{\infty}\frac{1}{n} < \sum_{n=1}^{\infty}\frac{n}{n^2+1}$

We know that the $\sum_{n=1}^{\infty}\frac{1}{n}$ is divergent. Therefore by the Comparison Test:

$\sum_{n=1}^{\infty}\frac{n}{n^2+1}$ is divergent.

Report an Error

Example Question #123 : Convergence And Divergence

Is the series

$\small \sum_{n=1}^\infty \frac{n^3}{n^7+1000}$

convergent or divergent, and why?

Possible Answers:

Divergent, by the test for divergence.

Divergent, by the comparison test.

Convergent, by the ratio test.

Divergent, by the ratio test.

Convergent, by the comparison test.

Correct answer:

Convergent, by the comparison test.

Explanation:

We will use the comparison test to prove that

$\small \sum_{n=1}^\infty \frac{n^3}{n^7+1000}$

converges (Note: we cannot use the ratio test, because then the ratio will be $\small 1$ , which means the test is inconclusive).

We will compare $\small \frac{n^3}{n^7+1000}$ to $\small \frac{1}{n^4}$ because they "behave" somewhat similarly. Both series are nonzero for all $\small n\geq 1$ , so one of the conditions is satisfied.

The series

$\small \small \sum_{n=1}^\infty \frac{1}{n^4}$

converges, so we must show that

$\small \small \frac{1}{n^4}\geq \frac{n^3}{n^4+1000}$

for $\small n\geq 1$ .

This is easy to show because

$\small \frac{1}{n^4}=\frac{n^3}{n^7}\geq \frac{n^3}{n^7+1000}$

since the denominator $\small n^7+1000$ is greater than or equal to $\small n^7$ for all $\small n\geq 1$ .

Thus, since

$\small \small \frac{1}{n^4}\geq \frac{n^3}{n^4+1000}$

and because

$\small \small \sum_{n=1}^\infty \frac{1}{n^4}$

converges, it follows that

$\small \sum_{n=1}^\infty \frac{n^3}{n^7+1000}$

converges, by comparison test.

Report an Error

Example Question #11 : Series Of Constants

Determine if the series converges or diverges. You do not need to find the sum.

$\sum_{n = 1}^{\infty } \frac{1}{n^{3} + 2}$

Possible Answers:

Neither converges nor diverges.

Converges

Conditionally converges.

Diverges

There is not enough information to decide convergence.

Correct answer:

Converges

Explanation:

We can compare this to the series $\sum_{n = 1}^{\infty } \frac{1}{n^{3}}$ which we know converges by the p-series test.

To figure this out, let's first compare $n^{3} + 2$ to $n^{3}$ . For any number n, $n^{3} + 2$ will be larger than $n^{3}$ .

There is a rule in math that if you take the reciprocal of each term in an inequality, you are allowed to flip the signs.

Thus, $n^{3} + 2 > n^{3}}$ turns into

$\frac{1}{n^{3}} > \frac{1}{n^{3} + 2}$ .

And so, because $\frac{1}{n ^{3}}$ converges, thus our series also converges.

Report an Error

Example Question #121 : Convergence And Divergence

For which values of p is

$\sum_{n=1}^\infty \frac{1}{n^p}$

convergent?

Possible Answers:

only p > 1

it doesn't converge for any values of

All positive values of

p=2

Correct answer:

only p > 1

Explanation:

We can solve this problem quite simply with the integral test. We know that if

$\int_1^{\infty} \frac{1}{x^p} dx$

converges, then our series converges.

We can rewrite the integral as

$\int x^{-p} dx$

and then use our formula for the antiderivative of power functions to get that the integral equals

$\frac{x^{1-p}}{1-p} \Big|_{x=1}^\infty$ .

We know that this only goes to zero if 1-p < 0 . Subtracting p from both sides, we get

1 < p .

Report an Error

Example Question #11 : Comparing Series

$\sum_{n=3}^{\infty}\frac{1}{n^2+2}$

Determine the convergence of the series using the Comparison Test.

Possible Answers:

Series diverges

Cannot be determined

Series converges

Correct answer:

Series converges

Explanation:

We compare this series to the series $\sum_{n=3}^{\infty}\frac{1}{n^2}$

Because

n^2+2>n^2 for n=3,4,5,...

it follows that

$\frac{1}{n^2+2}<\frac{1}{n^2}$ for n=3,4,5,...

This implies

$\sum_{n=3}^{\infty}\frac{1}{n^2+2}<\sum_{n=3}^{\infty}\frac{1}{n^2}$

Because the series on the right has an exponent 2>1 ,

the series on the right converges

$\sum_{n=3}^{\infty}\frac{1}{n^2+2}<\sum_{n=3}^{\infty}\frac{1}{n^2}=\frac{\pi^2}{6}-\frac{5}{4}$

making

$\sum_{n=3}^{\infty}\frac{1}{n^2+2}$

converge as well.

Report an Error

Example Question #2951 : Calculus Ii

$\sum_{n=2}^{\infty}\frac{1}{ln\,n}$

Determine the convergence of the series using the Comparison Test.

Possible Answers:

Series converges

Cannot be determined

Series diverges

Correct answer:

Series diverges

Explanation:

We compare this series to the series $\sum_{n=2}^{\infty}\frac{1}{n}$

Because

$ln\,n<n$ for n=2,3,4,...

it follows that

$\frac{1}{ln\,n}>\frac{1}{n}$ for n=2,3,4,...

This implies

$\sum_{n=2}^{\infty}\frac{1}{ln\,n}>\sum_{n=2}^{\infty}\frac{1}{n}$

Because the series on the right has a degree of equal to in the denominator,

the series on the right diverges

$\sum_{n=2}^{\infty}\frac{1}{n}>\infty$

making

$\sum_{n=2}^{\infty}\frac{1}{ln\,n}$

diverge as well.

Report an Error

Example Question #2952 : Calculus Ii

Does the series $\sum_{n=1}^\infty\frac{1}{n(n+1)}$ converge or diverge? If it does converge, then what value does it converge to?

Possible Answers:

Diverges

Converges to 1

Converges to $\sqrt2$

Converges to $\frac{1}{2}$

Converges to $\frac{\sqrt2}{2}$

Correct answer:

Converges to 1

Explanation:

To show this series converges, we use direct comparison with

$\sum_{n=1}^\infty\frac{1}{n^2}$ ,

which converges by the p-series test with p=2>1 .

Thus we must show that

$\frac{1}{n(n+1)}\le\frac{1}{n^2}$ .

Cross multiplying the previous section and multiplying by n+1 , we obtain $n^2\le{n^2+n}\leftrightarrow{n\ge0}$ .

Since this holds for all n=1,2,3,... we can conclude that

$\frac{1}{n(n+1)}\le\frac{1}{n^2}$ .

Summing from to $\infty$ , and noting that

$\frac{1}{n(n+1)}>0$ for all n=1,2,3,... , we obtain the following inequality:

$0<\sum_{n=1}^\infty\frac{1}{n(n+1)}<\sum_{n=1}^\infty\frac{1}{n^2}$ .

Therefore the series

$\sum_{n=1}^\infty\frac{1}{n(n+1)}$

converges by direct comparison.

Now to find the value, we note that

$\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$ ,

so that

$\sum_{n=1}^\infty\frac{1}{n(n+1)}=\sum_{n=1}^\infty\biggr(\frac{1}{n}-\frac{1}{n+1}\biggr)$ .

Now let

$s_k=\sum_{n=1}^k\biggr(\frac{1}{n}-\frac{1}{n+1}\biggr)$

be a sequence of partial sums.

Then we have $s_k=\sum_{n=1}^k\biggr(\frac{1}{n}-\frac{1}{n+1}\biggr)$

$=\biggr(1-\frac{1}{2}\biggr)+\biggr(\frac{1}{2}-\frac{1}{3}\biggr)+\biggr(\frac{1}{3}-\frac{1}{4}\biggr)+...+\biggr(\frac{1}{k-1}-\frac{1}{k}\biggr)$

$=1-\frac{1}{k}$

Therefore

$s_k=1-\frac{1}{k}$ .

Taking the limit as $k\rightarrow\infty$ , we obtain the following:

$\lim_{k\rightarrow\infty}s_k=\lim_{k\rightarrow\infty}\sum_{n=0}^k\frac{1}{n(n+1)}=\sum_{n=0}^\infty\frac{1}{n(n+1)}=\lim_{k\rightarrow\infty}\biggr(1-\frac{1}{k}\biggr)=1-\frac{1}{\infty}=1$

Therefore we have

$\sum_{n=0}^\infty\frac{1}{n(n+1)}=1$ .

Report an Error

Example Question #131 : Convergence And Divergence

Does the series converge?

$\sum_{n=2}^{\infty}\frac{1}{n-1}$

Possible Answers:

Yes

Cannot be determined

Correct answer:

Explanation:

Notice that n-1<n for n=2,3,...

This implies that

$\frac{1}{n-1}>\frac{1}{n}$ for n=2,3,...

Which then implies

$\sum_{n=2}^{\infty}\frac{1}{n-1}>\sum_{n=2}^{\infty}\frac{1}{n}$

Since the right-hand side is the harmonic series, we have

$\sum_{n=2}^{\infty}\frac{1}{n-1}> \infty$

and thus the series does NOT converge.

Report an Error

Example Question #12 : Comparing Series

Determine whether the series converges, absolutely, conditionally or in an interval.

$\sum_{n=0}^{\infty}\sqrt{n+1}-\sqrt{n}$

Possible Answers:

Converges in an interval

Converges conditionally

Does not converge at all

Converges absolutely

Correct answer:

Converges absolutely

Explanation:

Untitled

Report an Error

Example Question #13 : Comparing Series

Determine whether the series converges

$\sum_{n=0}^{\infty}\frac{1+\cos n}{3^n}$

Possible Answers:

Does not converge at all

Converges in an interval

Converges absolutely

Converges conditionally

Correct answer:

Converges absolutely

Explanation:

Untitled

Report an Error

View Calculus 2 Tutors

Philipp
Certified Tutor

University of Nevada-Las Vegas, Bachelor of Science, Mechanical Engineering.

View Calculus 2 Tutors

Andrew
Certified Tutor

Louisiana State University Eunice, Bachelor of Science, Computer Software Engineering.

View Calculus 2 Tutors

Reuben
Certified Tutor

University of Alberta, Bachelor of Science, Mathematics.

All Calculus 2 Resources

9 Diagnostic Tests 308 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GMAT Tutors in San Francisco-Bay Area, Spanish Tutors in Atlanta, Calculus Tutors in San Francisco-Bay Area, LSAT Tutors in Houston, ISEE Tutors in Phoenix, Chemistry Tutors in Seattle, Computer Science Tutors in Miami, Statistics Tutors in Philadelphia, Statistics Tutors in Houston, Math Tutors in Boston

Popular Courses & Classes

GRE Courses & Classes in Philadelphia, SAT Courses & Classes in Chicago, SSAT Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in Houston, SAT Courses & Classes in Seattle, Spanish Courses & Classes in Denver, GMAT Courses & Classes in Philadelphia, ACT Courses & Classes in Denver, ISEE Courses & Classes in Houston, SSAT Courses & Classes in Chicago

Popular Test Prep

SSAT Test Prep in Washington DC, LSAT Test Prep in San Diego, ACT Test Prep in Boston, GMAT Test Prep in Atlanta, GMAT Test Prep in Miami, GMAT Test Prep in Dallas Fort Worth, GRE Test Prep in Los Angeles, SSAT Test Prep in Houston, ACT Test Prep in Denver, ISEE Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Calculus 2 : Comparing Series

Study concepts, example questions & explanations for Calculus 2

All Calculus 2 Resources

Example Questions

Example Question #161 : Series In Calculus

Example Question #123 : Convergence And Divergence

Example Question #11 : Series Of Constants

Example Question #121 : Convergence And Divergence

Example Question #11 : Comparing Series

Example Question #2951 : Calculus Ii

Example Question #2952 : Calculus Ii

Example Question #131 : Convergence And Divergence

Example Question #12 : Comparing Series

Example Question #13 : Comparing Series

All Calculus 2 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: