All Calculus 2 Resources
Example Questions
Example Question #22 : Taylor Series
Write out the first three terms of the Taylor series about for the following function:
The general formula for the Taylor series about x=a for a given function is
We must find the zeroth, first, and second derivative of the function (for n=0, 1, and 2). The zeroth derivative is just the function itself.
The derivatives were found using the following rule:
Now, follow the above formula to write out the first three terms:
which simplified becomes
Example Question #11 : Taylor Series
Write out the first three terms of the Taylor series about for the following function:
The Taylor series about x=a for a function is given by
For the first three terms (n=0, 1, 2) we must find the zeroth, first, and second derivative of the function. The zeroth derivative is just the function itself.
The derivatives were found using the following rules:
,
Now, using the above formula, write out the first three terms:
which simplified becomes
Example Question #12 : Taylor Series
Write out the first three terms of the Taylor series about for the following function:
The Taylor series about x=a for a function is
For the first three terms (n=0, 1, 2), we must find the zeroth, first, and second derivative, where the zeroth derivative is just the function itself:
The derivatives were found using the following rules:
,
Now, using the above formula, write out the first three terms:
which simplified becomes
.
Example Question #13 : Taylor Series
Write out the first two terms of the Taylor series about for the following function:
The Taylor series about x=a for a function is given by
Now, for the first two terms (n=0, 1) we must find the zeroth and first derivative of the function, the zeroth derivative being the function itself:
The derivative was found using the following rules:
,
,
Now, use the above formula to write out the first two terms:
which simplified becomes
Example Question #14 : Taylor Series
Write out the first four terms of the Taylor series about for the following function:
The Taylor series about x=a for a function is
For the first four terms (n=0, 1, 2, 3), we must find the zeroth, first, second, and third derivative of the function. The zeroth derivative is the function itself.
The derivatives were found using the following rule:
Now, use the above formula to write out the first four terms:
which simplified becomes
.
Example Question #15 : Taylor Series
Write out the first three terms of the Taylor series about for the following function:
The Taylor series about x=a for a given function is
So, for the first three terms (n=0, 1, 2), we must find the zeroth, first, and second derivatives of the function, where the zeroth derivative is just the function itself:
The derivatives were found using the following rules:
,
,
,
,
Now, using the above formula, write out the first three terms:
which simplified becomes
.
Example Question #16 : Taylor Series
Write out the first four terms for the Taylor series about for the following function:
The Taylor series about x=a for a funtion is given by
For the first four terms (n=0, 1, 2, 3), we must find the zeroth, first, second, and third derivative of the function, where the zeroth derivative is just the function itself:
The derivatives were found using the following rules:
, ,
Now, use the above formula to write out the first four terms (after some distribution we get the final answer):
which simplified becomes
Example Question #17 : Taylor Series
Write out the first two terms of the Taylor series about for the following function:
The Taylor series about x=a for a function is given by
First, we must find the zeroth and first derivative of the function (n=0, 1), where the zeroth derivative is just the function itself:
and was found using the following rules:
,
,
,
Now, use the above formula to write out the first two terms:
which simplified becomes
Example Question #11 : Taylor And Maclaurin Series
Write out the first three terms of the Taylor series about for the following function:
The Taylor series about x=a for a function is given by
For the first three terms (n=0, 1, 2) we must find the zeroth, first, and second derivative of the function, where the zeroth derivative is just the function itself:
The derivatives were found using the following rules:
,
,
,
,
Now, write out the first three terms using the above formula:
which simplified becomes
Example Question #18 : Taylor Series
What is the power series of the function below?
It is known that the power series for at is
So we just need to plug this in with instead of to get
Certified Tutor
Certified Tutor
All Calculus 2 Resources













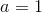

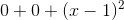
![0+(1+e^1)+[(2+e^1)(x-1)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/436358/gif.latex)
![(1+e^1)+[(2+e^1)(x-1)]+(x-1)^2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/436356/gif.latex)
![(1+e^1)+[(2+e^1)(x-1)]+\frac{(2+e^1)(x-1)^2}{2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/436360/gif.latex)

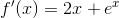



![\frac{(1+e^1)(x-1)^0}{0!}+\frac{[(2+e^1)(x-1)^1]}{1!}+\frac{(2+e^1)(x-1)^2}{2!}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/436367/gif.latex)
![(1+e^1)+[(2+e^1)(x-1)]+\frac{(2+e^1)(x-1)^2}{2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/436368/gif.latex)




















































































































