All College Chemistry Resources
Example Questions
Example Question #1 : Gases
One flask is at STP and another is at 
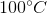
Possible Answers:
Correct answer:
Explanation:
The pressure of the flask at 

Because the volume between the flasks and the moles in each flask are constant, we can cancel out 

At STP, conditions are 

Example Question #41 : Solutions, States Of Matter, And Thermochemistry
A 3.00 L container at 273 K is filled with 1.00 mol Cl2(g), which behaves non-ideally.
Using the van der Waals equation, calculate pressure exerted by the gas.

Possible Answers:
Correct answer:
Explanation:
Recall the van der Waals equation for non-ideal gases
Rewrite the equation using the known values and solve for P
All College Chemistry Resources
Popular Subjects
SAT Tutors in Seattle, MCAT Tutors in Chicago, Calculus Tutors in New York City, English Tutors in Washington DC, Algebra Tutors in Washington DC, Computer Science Tutors in Atlanta, Biology Tutors in New York City, English Tutors in Phoenix, English Tutors in Seattle, English Tutors in San Francisco-Bay Area
Popular Courses & Classes
LSAT Courses & Classes in Houston, GRE Courses & Classes in Philadelphia, SSAT Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Miami, ISEE Courses & Classes in Houston, ISEE Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Boston, SAT Courses & Classes in Denver, GRE Courses & Classes in Los Angeles

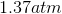

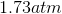

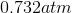


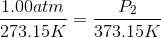



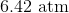



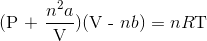
![[\textrm{P + }\frac{(1\textrm{ mol})^{2}(6.49\frac{\textrm{L}^{2}\textrm{ atm}}{\textrm{mol}^{2}})}{(3.00\textrm{ L})^2}][\textrm{3.00 L - (1 mol)}(0.0562\frac{\textrm{L}}{\textrm{mol}})]=(1\textrm{ mol})^{2}(0.0821\frac{\textrm{atm}}{\textrm{mol K}})(273K)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/996927/gif.latex)





