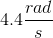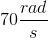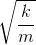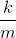First let's write out the information we are given:

We know that in order to obtain the time it takes a projectile to hit the ground we just multiply  by , since the time it takes to reach the max height is half of the total time the project is in the air, so 

Now we can use the equation 

Since we are only concerned with the particle's motion in the horizontal direction, and we know that the horizontal velocity is constant . We also know  since that is the definition of the initial position.

This gives us:

Let's plug in what we have:

. This is the range and our final answer. The reason why we can just use  as the horizontal velocity is because the project is launched at a ° angle. 

There are many explanations for this. First you could simply insert a velocity at all of these angles and see which ends up with the greatest change in horizontal distance. You also could use basic calculus and solve for the greatest theta.

This is a projectile motion problem. The problem states that it was thrown off the building at an angle of 30 degrees to the horizontal. So before we can find time, we need to find the horizontal and vertical parts of this velocity. 

Since   and 

It follows that 

Now, before we can find far it went, we need to find how long it was in the air. We need to solve for time.

With the equation   we can find t.

X is the initial height which in this case is the  tall building. V is the initial vertical velocity  and  

Plugging all that in and solving yields 

Knowing that the time the ball is in the air is  and the constant horizontal velocity is , we can plug in these known values into the simple distance formula to solve for distance.

The angular frequency of a simple pendulum is , where is the length of the pendulum.

For this question, we need to recall what simple harmonic motion is. Remember that it is a periodic motion where the restoring force depends on the displacement of the object undergoing these motions. So to answer this question, we need to keep this idea in mind and see which example doesn't match up.

A mass on a pendulum moving back and forth is clearly an example of simple harmonic motion. As the mass moves further from the center in either direction, it experiences a greater and greater force in the opposite direction.

A child swinging on a swing set is another correct example. This situation is analogous to the mass on a pendulum swinging back and forth.

A vibrating guitar string is yet another example of simple harmonic motion. After it is plucked, the string oscillates back and forth.

Finally, a book falling to the ground does not represent harmonic motion. Once the book is released from rest, we intuitively know that it will fall to the ground and will then stay there; in no way is there any periodic motion.

We know that the equation for the period of a simple pendulum is . This equation does not depend on mass. It is only affected by the length of the pendulum (L) and the gravitational constant (g). Therefore, adding mass to the pendulum will not effect the period, so the period remains the same.

Since we are solving for string tension, we need to use the frequency equation with the tension variable in it. That equation is  where  is the frequency,  is the number of the harmonic,  is the length of the string,  is the linear density of the string, and  is the tension of the string.

We are given:

Next we must convert the length of  to meters which is  and the mass density of  to . Then we plug in our known values into the equation and solve for the string tension. The result is .

We know that T is the period. The equation for T is  for harmonic motion.

Solve for  by dividing the equation by on both sides. The result is , which is the answer.

First, we need to find the length of the pendulum. Begin with the equation for finding the period of a pendulum:

solve for  to get:

Now we can plug in our given values:

Since we have the length of the pendulum determined, we can now find the period of the pendulum on Mars: