All Common Core: 3rd Grade Math Resources
Example Questions
Example Question #111 : Measurement And Estimation
Megan is working on a science experiment. Using the scale below, how much water will she have if she adds 

Megan has 

Example Question #112 : Measurement And Estimation
Megan is working on a science experiment. She needs to evenly divide the water shown in the beaker below into 

Megan has 




Example Question #113 : Measurement And Estimation
Megan is working on a science experiment. She needs to evenly divide the water shown in the beaker below into 

Megan has 




Example Question #114 : Measurement And Estimation
Megan is working on a science experiment. She needs to evenly divide the water shown in the beaker below into 

Megan has 




Example Question #115 : Measurement And Estimation
Megan is working on a science experiment. She needs 

Megan has 

Example Question #116 : Measurement And Estimation
Megan is working on a science experiment. She needs 

Megan has 

Example Question #117 : Measurement And Estimation
Megan is working on a science experiment. She needs to have 

Megan has 

Example Question #118 : Measurement And Estimation
Megan is working on a science experiment. She needs to have 

Megan has 

Example Question #11 : Measure Volume And Solve One Step Word Problems Involving Volume: Ccss.Math.Content.3.Md.A.2
Megan is working on a science experiment. She needs to have 

Megan has 

Example Question #12 : Measure Volume And Solve One Step Word Problems Involving Volume: Ccss.Math.Content.3.Md.A.2
Megan is working on a science experiment. She needs 

Megan has 

All Common Core: 3rd Grade Math Resources































![\frac{\begin{array}[b]{r}15\\ \times\ 4\end{array}}{ \ \ \ \ \space 60g}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/586778/gif.latex)





![\frac{\begin{array}[b]{r}19\\ \times\ 4\end{array}}{ \ \ \ \space 76g}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/586805/gif.latex)















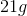
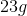






![\frac{\begin{array}[b]{r}11\\ \times\ 4\end{array}}{ \ \ \ \ \ \space 44g}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/586790/gif.latex)



