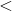All Common Core: 4th Grade Math Resources
Example Questions
Example Question #21 : Extend Understanding Of Fraction Equivalence And Ordering
Select the fraction that is equivalent to






Notice that when we line up our fraction models, which are the exact same size, the same portion of the rectangle is filled in.


Also, notice that 
Example Question #22 : Extend Understanding Of Fraction Equivalence And Ordering
Select the fraction that is equivalent to






Notice that when we line up our fraction models, which are the exact same size, the same portion of the rectangle is filled in.


Also, notice that 
Example Question #21 : Extend Understanding Of Fraction Equivalence And Ordering
Select the fraction that is equivalent to






Notice that when we line up our fraction models, which are the exact same size, the same portion of the rectangle is filled in.


Also, notice that 

Example Question #22 : Number & Operations: Fractions
Select the fraction that is equivalent to






Notice that when we line up our fraction models, which are the exact same size, the same portion of the rectangle is filled in.


Also, notice that 

Example Question #1 : How To Compare Fractions
Select the symbol to correctly fill in the blank below.

To compare fractions, we need to first make common denominators.
Now that we have common denominators, we can compare numerators. The fraction with the bigger numerator has the greater value.
Example Question #321 : Fractions
Select the symbol to correctly fill in the blank below.

To compare fractions, we need to first make common denominators.
Now that we have common denominators, we can compare numerators. The fraction with the bigger numerator has the greater value.
Example Question #2 : Compare Two Fractions With Different Numerators And Different Denominators: Ccss.Math.Content.4.Nf.A.2
Select the symbol to correctly fill in the blank below.

To compare fractions, we need to first make common denominators.
Now that we have common denominators, we can compare numerators. The fraction with the bigger numerator has the greater value.
Example Question #23 : Extend Understanding Of Fraction Equivalence And Ordering
Select the symbol to correctly fill in the blank below.

To compare fractions, we need to first make common denominators.
Now that we have common denominators, we can compare numerators. The fraction with the bigger numerator has the greater value.
Example Question #1 : How To Compare Fractions
Select the symbol to correctly fill in the blank below.

To compare fractions, we need to first make common denominators.
Now that we have common denominators, we can compare numerators. The fraction with the bigger numerator has the greater value.
Example Question #2 : How To Compare Fractions
Select the symbol to correctly fill in the blank below.

To compare fractions, we need to first make common denominators.
Now that we have common denominators, we can compare numerators. The fraction with the bigger numerator has the greater value.
Certified Tutor
Certified Tutor
All Common Core: 4th Grade Math Resources