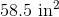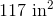All Common Core: 6th Grade Math Resources
Example Questions
Example Question #1 : Find Area Of Polygons: Ccss.Math.Content.6.G.A.1
What is the area of the right triangle in the following figure?

There are several different ways to solve for the area of a right triangle. In this lesson, we will transform the right triangle into a rectangle, use the the simpler formula for area of a rectangle to solve for the new figure's area, and divide this area in half in order to solve for the area of the original figure.
First, let's transform the triangle into a rectangle:

Second, let's remember that the formula for area of a rectangle is as follows:
Substitute in our side lengths.
Last, notice that our triangle is exactly half the size of the rectangle that we made. This means that in order to solve for the area of the triangle we will need to take half of the area of the rectangle, or divide it by 
Thus, the area formula for a right triangle is as follows:

Example Question #44 : Triangles
What is the area of the right triangle in the following figure?

There are several different ways to solve for the area of a right triangle. In this lesson, we will transform the right triangle into a rectangle, use the the simpler formula for area of a rectangle to solve for the new figure's area, and divide this area in half in order to solve for the area of the original figure.
First, let's transform the triangle into a rectangle:

Second, let's remember that the formula for area of a rectangle is as follows:
Substitute in our side lengths.
Last, notice that our triangle is exactly half the size of the rectangle that we made. This means that in order to solve for the area of the triangle we will need to take half of the area of the rectangle, or divide it by 
Thus, the area formula for a right triangle is as follows:

Example Question #1 : Geometry
What is the area of the right triangle in the following figure?

There are several different ways to solve for the area of a right triangle. In this lesson, we will transform the right triangle into a rectangle, use the the simpler formula for area of a rectangle to solve for the new figure's area, and divide this area in half in order to solve for the area of the original figure.
First, let's transform the triangle into a rectangle:

Second, let's remember that the formula for area of a rectangle is as follows:
Substitute in our side lengths.
Last, notice that our triangle is exactly half the size of the rectangle that we made. This means that in order to solve for the area of the triangle we will need to take half of the area of the rectangle, or divide it by 
Thus, the area formula for a right triangle is as follows:

Example Question #1 : Geometry
What is the area of the right triangle in the following figure?

There are several different ways to solve for the area of a right triangle. In this lesson, we will transform the right triangle into a rectangle, use the the simpler formula for area of a rectangle to solve for the new figure's area, and divide this area in half in order to solve for the area of the original figure.
First, let's transform the triangle into a rectangle:

Second, let's remember that the formula for area of a rectangle is as follows:
Substitute in our side lengths.
Last, notice that our triangle is exactly half the size of the rectangle that we made. This means that in order to solve for the area of the triangle we will need to take half of the area of the rectangle, or divide it by 
Thus, the area formula for a right triangle is as follows:

Example Question #2 : Geometry
What is the area of the right triangle in the following figure?

There are several different ways to solve for the area of a right triangle. In this lesson, we will transform the right triangle into a rectangle, use the the simpler formula for area of a rectangle to solve for the new figure's area, and divide this area in half in order to solve for the area of the original figure.
First, let's transform the triangle into a rectangle:

Second, let's remember that the formula for area of a rectangle is as follows:
Substitute in our side lengths.
Last, notice that our triangle is exactly half the size of the rectangle that we made. This means that in order to solve for the area of the triangle we will need to take half of the area of the rectangle, or divide it by 
Thus, the area formula for a right triangle is as follows:

Example Question #11 : How To Find The Area Of A Triangle
What is the area of the right triangle in the following figure?

There are several different ways to solve for the area of a right triangle. In this lesson, we will transform the right triangle into a rectangle, use the the simpler formula for area of a rectangle to solve for the new figure's area, and divide this area in half in order to solve for the area of the original figure.
First, let's transform the triangle into a rectangle:

Second, let's remember that the formula for area of a rectangle is as follows:
Substitute in our side lengths.
Last, notice that our triangle is exactly half the size of the rectangle that we made. This means that in order to solve for the area of the triangle we will need to take half of the area of the rectangle, or divide it by 
Thus, the area formula for a right triangle is as follows:

Example Question #1 : Find Area Of Polygons: Ccss.Math.Content.6.G.A.1
What is the area of the right triangle in the following figure?

There are several different ways to solve for the area of a right triangle. In this lesson, we will transform the right triangle into a rectangle, use the the simpler formula for area of a rectangle to solve for the new figure's area, and divide this area in half in order to solve for the area of the original figure.
First, let's transform the triangle into a rectangle:

Second, let's remember that the formula for area of a rectangle is as follows:
Substitute in our side lengths.
Last, notice that our triangle is exactly half the size of the rectangle that we made. This means that in order to solve for the area of the triangle we will need to take half of the area of the rectangle, or divide it by 
Thus, the area formula for a right triangle is as follows:

Example Question #1 : Geometry
What is the area of the right triangle in the following figure?

There are several different ways to solve for the area of a right triangle. In this lesson, we will transform the right triangle into a rectangle, use the the simpler formula for area of a rectangle to solve for the new figure's area, and divide this area in half in order to solve for the area of the original figure.
First, let's transform the triangle into a rectangle:

Second, let's remember that the formula for area of a rectangle is as follows:
Substitute in our side lengths.
Last, notice that our triangle is exactly half the size of the rectangle that we made. This means that in order to solve for the area of the triangle we will need to take half of the area of the rectangle, or divide it by 
Thus, the area formula for a right triangle is as follows:

Example Question #12 : How To Find The Area Of A Triangle
What is the area of the right triangle in the following figure?

There are several different ways to solve for the area of a right triangle. In this lesson, we will transform the right triangle into a rectangle, use the the simpler formula for area of a rectangle to solve for the new figure's area, and divide this area in half in order to solve for the area of the original figure.
First, let's transform the triangle into a rectangle:

Second, let's remember that the formula for area of a rectangle is as follows:
Substitute in our side lengths.
Last, notice that our triangle is exactly half the size of the rectangle that we made. This means that in order to solve for the area of the triangle we will need to take half of the area of the rectangle, or divide it by 
Thus, the area formula for a right triangle is as follows:

Example Question #13 : How To Find The Area Of A Triangle
What is the area of the right triangle in the following figure?

There are several different ways to solve for the area of a right triangle. In this lesson, we will transform the right triangle into a rectangle, use the the simpler formula for area of a rectangle to solve for the new figure's area, and divide this area in half in order to solve for the area of the original figure.
First, let's transform the triangle into a rectangle:

Second, let's remember that the formula for area of a rectangle is as follows:
Substitute in our side lengths.
Last, notice that our triangle is exactly half the size of the rectangle that we made. This means that in order to solve for the area of the triangle we will need to take half of the area of the rectangle, or divide it by 
Thus, the area formula for a right triangle is as follows:

All Common Core: 6th Grade Math Resources