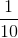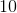All Common Core: 7th Grade Math Resources
Example Questions
Example Question #57 : Outcomes
Find the probability of drawing a heart from a deck of cards.
To find the probability of an event, we will use the following formula:
So, given the event of drawing heart, we can calculate the following:
because there are 13 ways we can draw a heart:
- Ace
- Two
- Three
- Four
- Five
- Six
- Seven
- Eight
- Nine
- Ten
- Jack
- Queen
- King
Now, we can calculate the following:
because there are 52 cards we could potentially draw from a deck of cards.
Knowing this, we can substitute into the formula. We get
Therefore, the probability of drawing a heart from a deck of cards is 
Example Question #58 : Outcomes
A box contains the following:
- 9 blue crayons
- 3 green crayons
- 4 red crayons
- 1 yellow crayon
Find the probability of grabbing a red crayon from the box.
To find the probability of an event, we will use the following formula:
Now, given the event of grabbing a red crayon from the box, we can calculate:
because there are 4 red crayons in the box we could grab.
We can also calculate:
because there are 17 total crayons we could potentially grab:
- 9 blue crayons
- 3 green crayons
- 4 red crayons
- 1 yellow crayon
So, we get
Therefore, the probability of grabbing a red crayon from the box is 
Example Question #59 : Outcomes
Find the probability that we draw a 5 from a deck of cards.
To find the probability of an event, we will use the following formula:
So, given the event of drawing a 5, we can calculate the following:
because there are 4 ways we can draw a 5 from a deck:
- 5 of clubs
- 5 of spades
- 5 of hearts
- 5 of diamonds
Now, we can calculate the following:
because there are 52 cards we could potentially draw from a deck of cards.
Knowing this, we can substitute into the formula. We get
Therefore, the probability of drawing a 5 from a deck of cards is 
Example Question #61 : How To Find The Probability Of An Outcome
If a class has 
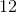
To find the probability of an event, we will use the following formula:
Now, in the event of calling on a boy in the class, we can determine the number of ways the event can happen:
because there are 10 boy students in the class.
To find the number of possible outcomes, we get
because there are 22 total students the teacher could potentially call on.
Knowing all of this, we can substitute into the formula. We get
Reduce:
Therefore, the probability of calling on a boy is 
Example Question #131 : Statistics & Probability
Megan has a bag of marbles containing 



In this problem we have a total of 



Megan wants to know what her probability is of drawing a pink marble out of her bag. Remember, probability is the number of favorable outcomes over the total number of outcomes:
For this problem there are 
Example Question #131 : Statistics & Probability
Megan has a bag of marbles containing 



In this problem we have a total of 



Megan wants to know what her probability is of drawing an orange marble out of her bag. Remember, probability is the number of favorable outcomes over the total number of outcomes:
For this problem there are 
Example Question #132 : Statistics & Probability
Megan has a bag of marbles containing 



In this problem we have a total of 



Megan wants to know what her probability is of drawing a green marble out of her bag. Remember, probability is the number of favorable outcomes over the total number of outcomes:
For this problem there are 
Example Question #4 : Develop A Uniform Probability Model By Assigning Equal Probability To All Outcomes: Ccss.Math.Content.7.Sp.C.7a
Megan has a bag of marbles containing 



In this problem we have a total of 



Megan wants to know what her probability is of drawing a yellow marble out of her bag. Remember, probability is the number of favorable outcomes over the total number of outcomes:
For this problem there are 
Example Question #1 : Develop A Uniform Probability Model By Assigning Equal Probability To All Outcomes: Ccss.Math.Content.7.Sp.C.7a
Samantha has a bag of marbles containing 







In this problem we have a total of 



Samantha wants to know what her probability is of drawing a orange marble out of her bag. Remember, probability is the number of favorable outcomes over the total number of outcomes:
For this problem there is 
Example Question #131 : Statistics & Probability
Samantha has a bag of marbles containing 







In this problem we have a total of 



Samantha wants to know what her probability is of drawing a pink marble out of her bag. Remember, probability is the number of favorable outcomes over the total number of outcomes:
For this problem there are 
Certified Tutor
Certified Tutor
All Common Core: 7th Grade Math Resources