All Common Core: 7th Grade Math Resources
Example Questions
Example Question #1 : Describe Situations In Which Opposite Quantities Combine To Make 0: Ccss.Math.Content.7.Ns.A.1a
Compute the following:
Convert all the double signs to a single sign before solving. Remember, two minus (negative) signs combine to form a plus (positive) sign, and a plus (positive) sign and a minus (negative) sign combine to form a minus (negative) sign.
Example Question #182 : Grade 7
For the equation provided, what value when substituted for 
In order to answer this question, we can solve for 


We can subtract 

Example Question #3 : Describe Situations In Which Opposite Quantities Combine To Make 0: Ccss.Math.Content.7.Ns.A.1a
For the equation provided, what value when substituted for 
In order to answer this question, we can solve for 


We can subtract 

Example Question #1 : Describe Situations In Which Opposite Quantities Combine To Make 0: Ccss.Math.Content.7.Ns.A.1a
For the equation provided, what value when substituted for 
In order to answer this question, we can solve for 


We can subtract 

Example Question #5 : Describe Situations In Which Opposite Quantities Combine To Make 0: Ccss.Math.Content.7.Ns.A.1a
For the equation provided, what value when substituted for 
In order to answer this question, we can solve for 


We can subtract 

Example Question #6 : Describe Situations In Which Opposite Quantities Combine To Make 0: Ccss.Math.Content.7.Ns.A.1a
For the equation provided, what value when substituted for 
In order to answer this question, we can solve for 


We can subtract 

Example Question #7 : Describe Situations In Which Opposite Quantities Combine To Make 0: Ccss.Math.Content.7.Ns.A.1a
For the equation provided, what value when substituted for 
In order to answer this question, we can solve for 


We can subtract 

Example Question #8 : Describe Situations In Which Opposite Quantities Combine To Make 0: Ccss.Math.Content.7.Ns.A.1a
For the equation provided, what value when substituted for 
In order to answer this question, we can solve for 


We can subtract 

Example Question #2 : Describe Situations In Which Opposite Quantities Combine To Make 0: Ccss.Math.Content.7.Ns.A.1a
For the equation provided, what value when substituted for 
In order to answer this question, we can solve for 


We can subtract 

Example Question #1 : The Number System
For the equation provided, what value when substituted for 
In order to answer this question, we can solve for 


We can subtract 

Certified Tutor
Certified Tutor
All Common Core: 7th Grade Math Resources






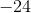









![\frac{\begin{array}[b]{r}11+x=0\\ -11\ \ \ \ -11\end{array}}{\\\\x=-11}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/913177/gif.latex)






![\frac{\begin{array}[b]{r}24+x=0\\ -24\ \ \ \ -24\end{array}}{\\\\x=-24}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/913198/gif.latex)






![\frac{\begin{array}[b]{r}38+x=0\\ -38\ \ \ \ -38\end{array}}{\\\\x=-38}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/913145/gif.latex)






![\frac{\begin{array}[b]{r}62+x=0\\ -62\ \ \ \ -62\end{array}}{\\\\x=-62}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/913221/gif.latex)






![\frac{\begin{array}[b]{r}70+x=0\\ -70\ \ \ \ -70\end{array}}{\\\\x=-70}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/913224/gif.latex)






![\frac{\begin{array}[b]{r}86+x=0\\ -86\ \ \ \ -86\end{array}}{\\\\x=-86}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/913120/gif.latex)






![\frac{\begin{array}[b]{r}99+x=0\\ -99\ \ \ \ -99\end{array}}{\\\\x=-99}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/913562/gif.latex)






![\frac{\begin{array}[b]{r}59+x=0\\ -59\ \ \ \ -59\end{array}}{\\\\x=-59}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/913234/gif.latex)






![\frac{\begin{array}[b]{r}19+x=0\\ -19\ \ \ \ -19\end{array}}{\\\\x=-19}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/913482/gif.latex)



