Solve the first equation for \(\displaystyle y\):

\(\displaystyle 3x+2y=12\)

\(\displaystyle 2y=12-3x\)

\(\displaystyle y=6-\frac{3}{2}x\)

Substitute into the second equation:

\(\displaystyle 4x-3(6-\frac{3}{2}x)=-1\)

\(\displaystyle 4x-18+\frac{9}{2}x=-1\)

Multiply the entire equation by 2 to eliminate the fraction:

\(\displaystyle 8x-36+9x=-2\)

\(\displaystyle 17x-36=-2\)

\(\displaystyle 17x=34\)

\(\displaystyle x=2\)

Using the value of \(\displaystyle x\), solve for \(\displaystyle y\):

\(\displaystyle 3(2)+2y=12\)

\(\displaystyle 6+2y=12\)

\(\displaystyle 2y=6\)

\(\displaystyle y=3\)

Therefore, the solution is \(\displaystyle \left ( 2,3 \right )\)

Set the two equations equal to one another:

2x - 2 = 3x + 6

Solve for x:

x = -8

Plug this value of x into either equation to solve for y.  We'll use the top equation, but either will work.

y = 2 * (-8) - 2

y = -18

Multiply the bottom equation by \(\displaystyle 5\), then add to the top equation:

\(\displaystyle 6x-y = -9\)

\(\displaystyle 5 \left (6x-y \right ) =5\cdot (-9)\)

\(\displaystyle 30x-5y = -45\)

\(\displaystyle \underline{\textrm{\; } 3x + 5y = \; \; 23}\)

\(\displaystyle 33x \;\;\;\;\;\; \; =-22\)

Divide both sides by \(\displaystyle 33\)

\(\displaystyle \frac{33x}{33}=-\frac{22}{33}\)

\(\displaystyle \frac{22}{33}=-\frac{2}{3}\)

When we add the two equations, the \(\displaystyle y\) variables cancel leaving us with:

\(\displaystyle 8x=-8\)

Solving for \(\displaystyle x\) we get:

\(\displaystyle \frac{8x}{8}=\frac{-8}{8}\)

\(\displaystyle x=-1\)

We can then substitute our value for \(\displaystyle x\) into one of the original equations and solve for \(\displaystyle y\):

\(\displaystyle \begin{matrix} -4-2y=-3\\ -4+4-2y=-3+4\\ -2y=1\\ y=-\frac{1}{2}\\ \end{matrix}\)

We are given

\(\displaystyle y=-3x+1\)

\(\displaystyle y=2x-9\)

We can solve this by using the substitution method.  Notice that you can plug \(\displaystyle -3x+1\) from the first equation into the second equation and then get

\(\displaystyle -3x+1=2x-9\)

Add \(\displaystyle 3x\) to both sides

\(\displaystyle -3x+3x+1=2x+3x-9\)

\(\displaystyle 1=5x-9\)

Add 9 to both sides

\(\displaystyle 1+9=5x-9+9\)

\(\displaystyle 10=5x\)

Divide both sides by 5

\(\displaystyle \frac{10}{5}=\frac{5x}{5}\)

\(\displaystyle 2=x\)

So \(\displaystyle x=2\). We can use this value to find y by using either equation. In this case, I'll use \(\displaystyle y=-3x+1\).

\(\displaystyle y=-3(2)+1\)

\(\displaystyle y=-6+1\)

\(\displaystyle y=-5\)

So the solution is 

\(\displaystyle (x,y)=(2,-5)\)

There are a couple of ways to solve a system of linear equations: graphically and algebraically. In this lesson, we will review the two ways to solve a system of linear equations algebraically: substitution and elimination. 

Substitution can be used by solving one of the equations for either \(\displaystyle x\) or \(\displaystyle y\), and then substituting that expression in for the respective variable in the second equation. You could also solve both equations so that they are in the \(\displaystyle y=\) form, and then set both equations equal to each other. 

Elimination is best used when one of the variables has the same coefficient in both equations, because you can then use addition or subtraction to cancel one of the variables out, and solve for the other variable. 

For this problem, elimination makes the most sense because our \(\displaystyle y\) variables have the same coefficient. We can add our equations together to cancel out the \(\displaystyle y\textup:\)

\(\displaystyle \frac{\begin{array}[b]{r}-7x-y=4\\ +\ 4x+y=-7\end{array}}{ -3x=-3}\)

Next, we can divide both sides by \(\displaystyle -3\) to solve for \(\displaystyle x\textup:\)

\(\displaystyle \frac{-3x}{-3}=\frac{-3}{-3}\)

\(\displaystyle x=1\)

Remember, when we are solving a system of linear equations, we are looking for the point of intersection; thus, our answer should have both \(\displaystyle x\) and \(\displaystyle y\) values. 

Now that we have the value of \(\displaystyle x\), we can plug that value into the \(\displaystyle x\) variable in one of our given equations and solve for \(\displaystyle y\textup:\)

\(\displaystyle 4(1)+y=-7\)

\(\displaystyle 4+y=-7\)

We want to subtract \(\displaystyle 4\) from both sides to isolate the \(\displaystyle y\textup:\)

\(\displaystyle \frac{\begin{array}[b]{r}4+y=-7\\ \ -4\ \ \ \ \ \ \ \ -4\end{array}}{\\\\y=-11}\)

Our point of intersection, and the solution to the two system of linear equations is \(\displaystyle (1,-11)\)

There are a couple of ways to solve a system of linear equations: graphically and algebraically. In this lesson, we will review the two ways to solve a system of linear equations algebraically: substitution and elimination. 

Substitution can be used by solving one of the equations for either \(\displaystyle x\) or \(\displaystyle y\), and then substituting that expression in for the respective variable in the second equation. You could also solve both equations so that they are in the \(\displaystyle y=\) form, and then set both equations equal to each other. 

Elimination is best used when one of the variables has the same coefficient in both equations, because you can then use addition or subtraction to cancel one of the variables out, and solve for the other variable. 

For this problem, elimination makes the most sense because our \(\displaystyle y\) variables have the same coefficient. We can subtract our equations to cancel out the \(\displaystyle y\textup:\)

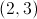
\(\displaystyle \frac{\begin{array}[b]{r}4x-4y=5\\ -\ 9x-4y=-15\end{array}}{ -5x=20}\)

Next, we can divide both sides by \(\displaystyle -5\) to solve for \(\displaystyle x\textup:\)

\(\displaystyle \frac{-5x}{-5}=\frac{20}{-5}\)

\(\displaystyle x=-4\)

Remember, when we are solving a system of linear equations, we are looking for the point of intersection; thus, our answer should have both \(\displaystyle x\) and \(\displaystyle y\) values. 

Now that we have the value of \(\displaystyle x\), we can plug that value into the \(\displaystyle x\) variable in one of our given equations and solve for \(\displaystyle y\textup:\)

\(\displaystyle 4(-4)-4y=5\)

\(\displaystyle -16-4y=5\)

We want to add \(\displaystyle 16\) to both sides to isolate the \(\displaystyle y\textup:\)

\(\displaystyle \frac{\begin{array}[b]{r}-16-4y=5\\ \ +16\ \ \ \ \ \ +16\end{array}}{\\\\-4y=21}\)

Then we divide each side by \(\displaystyle -4\textup:\)

\(\displaystyle \frac{-4y}{-4}=\frac{21}{-4}\)

\(\displaystyle y=-5\frac{1}{4}\)

Our point of intersection, and the solution to the two system of linear equations is \(\displaystyle (-4,-5\frac{1}{4})\)

There are a couple of ways to solve a system of linear equations: graphically and algebraically. In this lesson, we will review the two ways to solve a system of linear equations algebraically: substitution and elimination. 

Substitution can be used by solving one of the equations for either \(\displaystyle x\) or \(\displaystyle y\), and then substituting that expression in for the respective variable in the second equation. You could also solve both equations so that they are in the \(\displaystyle y=\) form, and then set both equations equal to each other. 

Elimination is best used when one of the variables has the same coefficient in both equations, because you can then use addition or subtraction to cancel one of the variables out, and solve for the other variable. 

For this problem, elimination makes the most sense because our \(\displaystyle y\) variables have the same coefficient. We can subtract our equations to cancel out the \(\displaystyle y\textup:\)

\(\displaystyle \frac{\begin{array}[b]{r}2x+2y=16\\ -\ 6x+2y=20\end{array}}{ -4x=-4}\)

Next, we can divide both sides by \(\displaystyle -4\) to solve for \(\displaystyle x\textup:\)

\(\displaystyle \frac{-4x}{-4}=\frac{-4}{-4}\)

\(\displaystyle x=1\)

Remember, when we are solving a system of linear equations, we are looking for the point of intersection; thus, our answer should have both \(\displaystyle x\) and \(\displaystyle y\) values. 

Now that we have the value of \(\displaystyle x\), we can plug that value into the \(\displaystyle x\) variable in one of our given equations and solve for \(\displaystyle y\textup:\)

\(\displaystyle 2(1)+2y=16\)

\(\displaystyle 2+2y=16\)

We want to subtract \(\displaystyle 2\) from both sides to isolate the \(\displaystyle y\textup:\)

\(\displaystyle \frac{\begin{array}[b]{r}2+2y=16\\ \ -2\ \ \ \ \ \ \ \ -2\end{array}}{\\\\2y=14}\)

Then divide both sides by \(\displaystyle 2\) to solve for \(\displaystyle y\text:\)

\(\displaystyle \frac{2y}{2}=\frac{14}{2}\)

\(\displaystyle y=7\)

Our point of intersection, and the solution to the two system of linear equations is \(\displaystyle (1,7)\)

There are a couple of ways to solve a system of linear equations: graphically and algebraically. In this lesson, we will review the two ways to solve a system of linear equations algebraically: substitution and elimination. 

Substitution can be used by solving one of the equations for either \(\displaystyle x\) or \(\displaystyle y\), and then substituting that expression in for the respective variable in the second equation. You could also solve both equations so that they are in the \(\displaystyle y=\) form, and then set both equations equal to each other. 

Elimination is best used when one of the variables has the same coefficient in both equations, because you can then use addition or subtraction to cancel one of the variables out, and solve for the other variable. 

For this problem, elimination makes the most sense because our \(\displaystyle y\) variables have the same coefficient. We can subtract our equations to cancel out the \(\displaystyle y\textup:\)

\(\displaystyle \frac{\begin{array}[b]{r}9x+3y=27\\ -\ 4x+3y=12\end{array}}{ 5x=15}\)

Next, we can divide both sides by \(\displaystyle 5\) to solve for \(\displaystyle x\textup:\)

\(\displaystyle \frac{5x}{5}=\frac{15}{5}\)

\(\displaystyle x=3\)

Remember, when we are solving a system of linear equations, we are looking for the point of intersection; thus, our answer should have both \(\displaystyle x\) and \(\displaystyle y\) values. 

Now that we have the value of \(\displaystyle x\), we can plug that value into the \(\displaystyle x\) variable in one of our given equations and solve for \(\displaystyle y\textup:\)

\(\displaystyle 4(3)+3y=12\)

\(\displaystyle 12+3y=12\)

We want to subtract \(\displaystyle 12\) from both sides to isolate the \(\displaystyle y\textup:\)

\(\displaystyle \frac{\begin{array}[b]{r}12+3y=12\\ \ -12\ \ \ \ \ \ \ \ -12\end{array}}{\\\\3y=0}\)

Then divide both sides by \(\displaystyle 3\) to solve for \(\displaystyle y\text:\)

\(\displaystyle \frac{3y}{3}=\frac{0}{3}\)

\(\displaystyle y=0\)

Our point of intersection, and the solution to the two system of linear equations is \(\displaystyle (3,0)\)

There are a couple of ways to solve a system of linear equations: graphically and algebraically. In this lesson, we will review the two ways to solve a system of linear equations algebraically: substitution and elimination. 

Substitution can be used by solving one of the equations for either \(\displaystyle x\) or \(\displaystyle y\), and then substituting that expression in for the respective variable in the second equation. You could also solve both equations so that they are in the \(\displaystyle y=\) form, and then set both equations equal to each other. 

Elimination is best used when one of the variables has the same coefficient in both equations, because you can then use addition or subtraction to cancel one of the variables out, and solve for the other variable. 

For this problem, elimination makes the most sense because our \(\displaystyle y\) variables have the same coefficient. We can subtract our equations to cancel out the \(\displaystyle y\textup:\)

\(\displaystyle \frac{\begin{array}[b]{r}-4x+y=20\\ -\ 6x+y=30\end{array}}{ -10x=-10}\)

Next, we can divide both sides by \(\displaystyle -4\) to solve for \(\displaystyle x\textup:\)

\(\displaystyle \frac{-10x}{-10}=\frac{-10}{-10}\)

\(\displaystyle x=1\)

Remember, when we are solving a system of linear equations, we are looking for the point of intersection; thus, our answer should have both \(\displaystyle x\) and \(\displaystyle y\) values. 

Now that we have the value of \(\displaystyle x\), we can plug that value into the \(\displaystyle x\) variable in one of our given equations and solve for \(\displaystyle y\textup:\)

\(\displaystyle 6(1)+y=30\)

\(\displaystyle 6+y=30\)

We want to subtract \(\displaystyle 2\) from both sides to isolate the \(\displaystyle y\textup:\)

\(\displaystyle \frac{\begin{array}[b]{r}6+y=30\\ \ -6\ \ \ \ \ \ \ \ -6\end{array}}{\\\\y=24}\)

Our point of intersection, and the solution to the two system of linear equations is \(\displaystyle (1,24)\)