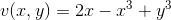Call Now to Set Up Tutoring:

(888) 888-0446

Complex Analysis : Analytic and Harmonic Functions

Study concepts, example questions & explanations for Complex Analysis

Create An Account

All Complex Analysis Resources

1 Diagnostic Test 13 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Analytic And Harmonic Functions

Find a Harmonic Conjugate v(x,y) of u(x,y) = 2x-x^3+3xy^2

Possible Answers:

v(x,y) = 2-3x^2+y^3

v(x,y) = 2x-x^3+y^3

v(x,y) = 2y-3x^2y+y^3

v(x,y) = 2y-x^2y + y^3

v(x,y) = 2y-x^3y+3xy^2

Correct answer:

v(x,y) = 2y-3x^2y+y^3

Explanation:

v(x,y) is said to be a harmonic conjugate of u(x,y) if their are both harmonic in their domain and their first order partial derivatives satisfy the Cauchy-Riemann Equations. Computing the partial derivatives

u_x(x,y) = 2-3x^2+3y^2 = v_y(x,y)

v(x,y) = 2y-3x^2y+y^3 + C

where is any arbitrary constant.

Report an Error

Example Question #2 : Analytic And Harmonic Functions

Given $f(z) = z - \bar{z}$ , where does f'(z) exist?

Possible Answers:

x = 0

z=0

Nowhere

y = 0

The Entire Complex Plane

Correct answer:

Nowhere

Explanation:

Rewriting f(z) in real and complex components, we have that

$f(z) = z- \bar{z} = (x+yi) - (x-yi) = 2yi$

So this implies that f(z) = f(x + yi) = u(x,y) + v(x,y)i

where $u(x,y) = 0 \text{ and } v(x,y) = 2y$

Therefore, checking the Cauchy-Riemann Equations, we have that

$u_x(x,y) = 0 \neq v_y(x,y) = 2$

So the Cauchy-Riemann equations are never satisfied on the entire complex plane, so f(z) is differentiable nowhere.

Report an Error

View Tutors

Candice
Certified Tutor

Grand Canyon University, Master's/Graduate, Elementary education .

View Tutors

Arvilla
Certified Tutor

Cazenovia College, Bachelor of Fine Arts, Graphic Design.

View Tutors

Matthew
Certified Tutor

Bluffton University, Bachelor of Education, Mathematics. Bluffton University, Masters in Education, Education.

All Complex Analysis Resources

1 Diagnostic Test 13 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in Los Angeles, Statistics Tutors in Los Angeles, Calculus Tutors in San Francisco-Bay Area, LSAT Tutors in Houston, Chemistry Tutors in Chicago, Calculus Tutors in Atlanta, French Tutors in Houston, Spanish Tutors in Phoenix, GRE Tutors in Seattle, Reading Tutors in Dallas Fort Worth

Popular Courses & Classes

MCAT Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Seattle, SSAT Courses & Classes in Houston, GMAT Courses & Classes in Seattle, MCAT Courses & Classes in Miami, GRE Courses & Classes in Washington DC, Spanish Courses & Classes in Boston, ISEE Courses & Classes in Atlanta, LSAT Courses & Classes in San Diego, LSAT Courses & Classes in Denver

Popular Test Prep

GMAT Test Prep in San Diego, SSAT Test Prep in Philadelphia, SAT Test Prep in Denver, MCAT Test Prep in Philadelphia, MCAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Atlanta, SSAT Test Prep in San Diego, SSAT Test Prep in Denver, SAT Test Prep in Houston, ISEE Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Complex Analysis : Analytic and Harmonic Functions

Study concepts, example questions & explanations for Complex Analysis

All Complex Analysis Resources

Example Questions

Example Question #1 : Analytic And Harmonic Functions

Example Question #2 : Analytic And Harmonic Functions

All Complex Analysis Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: