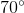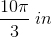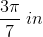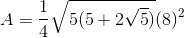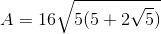All GRE Math Resources
Example Questions
Example Question #2 : How To Find The Area Of A Sector
What is the area of a sector of a circle of radius 4 that spans an arc of 86 degrees?
172/45 * ∏
1/5 * ∏
17/42 * ∏
12/53 * ∏
1/4 * ∏
172/45 * ∏
sector area = ∏ * r2 * degrees/360 = ∏ * 42 * 86/360 = 172/45 * ∏
Example Question #41 : Geometry
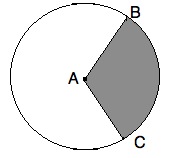
The circle above has a center of A, and points B and C lie on the circumference.
What is the area of the shaded region?
None of the other answers
We need to begin by finding the area of the following sector:
If ∠BAC = 120°, then the area of sector BAC is equal to 120 / 360 = 1/3 of the entire circle. Since AC is 12 and is a radius, we know the total area is pi *122 = 144*pi. The sector is then 144*pi / 3 = 48*pi.
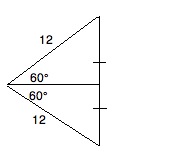
Now, we need to find the area of the triangle ABC. Since AB and AC are equal (both being radii of our circle), we have an icoseles triangle. If we drop a height from ∠BAC, we have the following triangle ABC:
We can use the 30-60-90 rule to find the height and base. One half of the base (x) is found by the following ratio:
√(3) / 2 = x / 12
Solving for x, we get: x = 6 * √(3). Therefore, the base is 12 * √(3).
To find the height (y), we use the following ratio:
1 / 2 = y / 12
Solving for y, we get y = 6.
Therefore, the area of the triangle = 0.5 * 6 * 12 * √(3) = 3 * 12 * √(3) = 36 * √(3)
The area of the shaded region is then 48*pi - 36 * √(3).
Example Question #1 : Clock Math
What is the angle between the hour and minute hand of a clock at 4:15?
In this case, the minute hand is pointing at 3 while the hour hand is pointing at some value past 4. Now, since 15 minutes represents 1/4 of an hour, the hour hand will be 1/4 the distance between 4 and 5. The total number of degrees between minutes is 360/12 = 30°; therefore, the hour hand is 30/4 or 7.5° past the 4 o'clock point. Now, between 3 and 4, there are 30°. Add to that the 7.5°. The total distance is therefore 37.5°.
Example Question #42 : Geometry
What is the angle, in degrees, between the minute and hour hands of the clock at 
To find the degrees between hands on a clock, you must first remember that a clockface is a circle, and therefore has an internal angle sum of 360 degrees. Since a clockface has a sum of 360 degrees and there are 12 numbers on a clockface, the degree difference between each number is 360 divided by 12, or 30 degrees.
You can use this 30 degrees to figure out the distance between the minute and hour hands at the time given. At 5:40pm, the minute hand will be on the 8, as each number indicates five minutes on the clock.
It is the hour hand where this calculation gets tricky. While it would be easy to assume that the hour hand would be on the 5 at this time, that's actually incorrect. The hour hand slowly creeps towards the next number throughout the hour, moving in appropriate increments to reflect the fraction of the hour that has past. Since 40 minutes is 2/3 of an hour, then the hour hand is 2/3 of the way towards the number 6 on 5:40pm.
Thus, when calculating the distance, you must find the difference between 5 2/3 and 8 on the clock.

Multiply this number by 30 (the degrees between each number on the clock, and thus the way we must convert this number to degrees), and you get 70 degrees.
Example Question #42 : Circles
A clock has two equally long hands on it, each measuring 


Our clock looks roughly like this:

Now, between every number on the clock, there are 




Now, we know:
We know that 
Example Question #45 : Geometry
A clock has two equally long hands on it, each measuring 



Our clock looks roughly like this:

Now, between every number on the clock, there are 










Now, we know:
We know that 
Example Question #41 : Geometry
A clock has two equally long hands on it, each measuring 


Our clock looks roughly like this:

Now, between every number on the clock, there are 





Now, we know:
We know that 
Example Question #1 : How To Find An Angle In A Hexagon
Quantitative Comparison
Quantity A: The degree measure of any angle in an equilateral triangle
Quantity B: The degree measure of any angle in a regular hexagon
The relationship cannot be determined from the information given.
The two quantities are equal.
Quantity B is greater.
Quantity A is greater.
Quantity B is greater.
We know the three angles in a triangle add up to 180 degrees, and all three angles are 60 degrees in an equilateral triangle.
A hexagon has six sides, and we can use the formula degrees = (# of sides – 2) * 180. Then degrees = (6 – 2) * 180 = 720 degrees. Each angle is 720/6 = 120 degrees.
Quantity B is greater.
Example Question #2 : How To Find An Angle In A Hexagon
Quantity A: Double the measure of a single interior angle of an equilateral triangle.
Quantity B: The measure of a single interior angle of a hexagon.
Quantity B is bigger.
Quantity A is bigger.
The relationship cannot be determined with the information given.
The quantities are equal.
The quantities are equal.
Begin with Quantity A. We know the measure of one angle in an equilateral triangle is 60. Therefore, double the angle is 120 degrees.
For the hexagon, use the formula for the sum of the interior angles:
where n= number of sides in a regular polygon
If the sum of the interior angles of a regular hexagon is 

The two quantities are equal.
Example Question #1 : Pentagons
The perimeter of a regular pentagon is 40 units. What is the area of the pentagon?
The formula for the area of a regular pentagon is given by the equation:
where a is represented by the length of one side. Let's begin by finding the side length of the regular pentagon. If the perimeter is 40, then we can divide by 5 (the number of sides) to find a side length of 8.
If we plug in 8 into the equation:
All GRE Math Resources